Выпуск 579

Лаборатория Наномир

Когда реальность открывает тайны,
уходят в тень и  меркнут чудеса ...

 Шкала индейцев победила шкалу папуасов.

Знаковый фрактал.

https://img-fotki.yandex.ru/get/44085/158289418.3a3/0_16b1db_7eb438aa_XL.jpg

На этой фотографии из музея мы видим структуру геодезической шкалы с периодом 288 узких полос. Напомню, что у папуасов я обнаружил шкалу с периодом 256 узких полос. Построим модель шкалы индейцев.

https://img-fotki.yandex.ru/get/197213/158289418.3a3/0_16b26f_d0c0d902_orig.jpg

Скрипт для 3DS Max:

-- Alien tool. Alexander Kushelev. Nanoworld. Lab
-- http://nanoworld.narod.ru
a = #(); num = #(
6,3,3,3,3,3,6,6,6,6,6,3,3,3,3,3 --16
,4,3,6,3,4,4,4,3,6,3,4 --27
,7,7,7,7,7,7,7,7,7,7 --37
,4,3,6,3,4,4,4,3,6,3,4 --48
,3,3,3,3,3,3,3,3,3 --57
,4,3,6,3,4,4,4,3,6,3,4 --68
,3,3,3,3,3,3,3,3,3 --77
,4,3,6,3,4,4,4,3,6,3,4 --88
,3,3,3,3,3,3,3,3,3 --97
,4,3,6,3,4,4,4,3,6,3,4 --108
,7,7,7,7,7,7,7,7,7,7 --118
,4,3,6,3,4,4,4,3,6,3,4 --129
,3,3,3,3,3,6,6,6,6,6,3,3,3,3,3 --144
,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4 --160
,4,3,6,3,4,4,4,3,6,3,4
,7,7,7,7,7,7,7,7,7,7
,4,3,6,3,4,4,4,3,6,3,4
,3,3,3,3,3,3,3,3,3
,4,3,6,3,4,4,4,3,6,3,4
,3,3,3,3,3,3,3,3,3
,4,3,6,3,4,4,4,3,6,3,4
,3,3,3,3,3,3,3,3,3
,4,3,6,3,4,4,4,3,6,3,4
,7,7,7,7,7,7,7,7,7,7
,4,3,6,3,4,4,4,3,6,3,4
,3,3,3,3,3,6,6,6,6,6,3,3,3,3,3)
x=0
-- black line
k=1
for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
--5 white lines
for k = 2 to 6 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
-- triangle
k = 7
a[55] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[56] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[57] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [255,255,255]
a[58] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[59] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[60] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[61] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 8
a[62] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[63] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[64] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[65] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[66] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[67] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[68] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 9
a[69] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [0,0,0]
a[70] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [0,0,0]
a[71] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[72] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[73] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[74] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[75] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 10
a[76] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[77] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[78] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[79] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[80] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[81] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[82] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 11
a[83] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[84] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[85] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [255,255,255]
a[86] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[87] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[88] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[89] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
--5 white lines
for k = 12 to 16 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
-- flag
for k = 17 to 27 do(
    for j = 1 to 2 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
for j = 3 to 5 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255])
for j = 6 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]))
--chess 
for k = 28 to 37 do(
    for j = 1 to 7 do(
If (mod(k+j) 2)/2 == 0 then    a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0] else a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
--red-white-black-white-3*red-white-black-white-red
for k = 38 to 108 do(
    for j = 1 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]
If num[k] == 7 then(
If (mod(k+j) 2)/2 == 0 then    a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0] else a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255])))
-- chess
for k = 109 to 118 do(
    for j = 1 to 7 do(
If (mod(k+j) 2)/2 == 0 then    a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0] else a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
-- flag
for k = 119 to 129 do(
    for j = 1 to 2 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
for j = 3 to 5 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255])
for j = 6 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]))
for k = 130 to 134 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
k = 135
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [255,255,255]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 136
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 137
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [0,0,0]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [0,0,0]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 138
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 139
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [255,255,255]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
for k = 140 to 144 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
k=145
for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
for k = 146 to 150 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
k = 151
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [255,255,255]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 152
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 153
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [0,0,0]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [0,0,0]
k = 154
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 155
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [255,255,255]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
for k = 156 to 160 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
-- flag
for k = 161 to 171 do(
    for j = 1 to 2 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
for j = 3 to 5 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255])
for j = 6 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]))
--chess 
for k = 172 to 181 do(
    for j = 1 to 7 do(
If (mod(k+j) 2)/2 == 0 then    a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0] else a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
--red-white-black-white-3*red-white-black-white-red
for k = 182 to 252 do(
    for j = 1 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]))
-- chess
for k = 253 to 262 do(
    for j = 1 to 7 do(
If (mod(k+j) 2)/2 == 0 then    a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0] else a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
-- flag
for k = 263 to 273 do(
    for j = 1 to 2 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0])
for j = 3 to 5 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255])
for j = 6 to 7 do(
if num[k] == 1 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,100,0] 
If num[k] == 2 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,0]
If num[k] == 3 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]
If num[k] == 4 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,0,0]
If num[k] == 5 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,255]
If num[k] == 6 then a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [0,0,0]))
for k = 274 to 278 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))
k = 279
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [255,255,255]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 280
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 281
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [0,0,0]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [0,0,0]
k = 282
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [0,0,0]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [0,0,0]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
k = 283
a[k*7-1] = sphere radius: 2.5 position:[5*1,5*k,0] wirecolor: [255,255,255]
a[k*7] = sphere radius: 2.5 position:[5*2,5*k,0] wirecolor: [255,255,255]
a[k*7+1] = sphere radius: 2.5 position:[5*3,5*k,0] wirecolor: [0,0,0]
a[k*7+2] = sphere radius: 2.5 position:[5*4,5*k,0] wirecolor: [255,255,255]
a[k*7+3] = sphere radius: 2.5 position:[5*5,5*k,0] wirecolor: [255,255,255]
a[k*7+4] = sphere radius: 2.5 position:[5*6,5*k,0] wirecolor: [255,255,255]
a[k*7+5] = sphere radius: 2.5 position:[5*7,5*k,0] wirecolor: [255,255,255]
for k = 284 to 288 do(
    for j = 1 to 7 do(
a[(k-1)*7+j] = sphere radius: 2.5 position:[5*j,5*k,0] wirecolor: [255,255,255]))

https://img-fotki.yandex.ru/get/194858/158289418.3a3/0_16b274_7b7d3045_orig.jpg

Шкала индейцев имеет не такой широкий масштабный диапазон, как шкала папуасов, но она удобна не только для измерения линейных, но и угловых величин. Увеличение периода вдвое получено за счёт использования нового типа фракталов. Назовём их Знаковыми фракталами. В отличие от других типов фракталов, в них используются знаки, что по существу позволяет делить фрактальные уровни. 

 Обсуждение

 Обсуждаем проект для Бумстартера

http://img-fotki.yandex.ru/get/9308/158289418.fa/0_c91b4_a6126539_orig.jpg

Описание проекта:

 

http://img-fotki.yandex.ru/get/4614/126580004.28/0_adf8a_a64d677f_XL.png
Рубиновый генератор рассчитан на 10 киловатт непрерывной мощности. Он сможет обогреть и осветить жилое или производственное помещение площадью до 100 квадратных метров. Ориентировочная цена 1000 рублей.

https://img-fotki.yandex.ru/get/15557/158289418.1a0/0_10250c_b17f5f00_XL.jpg

Принцип действия.
Рубиновый генератор создает условия преобразования вращательного движения элементов среды (эфира, вакуума) в колебательное (электромагнитные колебания). То же самое, но в другом масштабе происходит при дребезге шестеренчатого механизма.

http://nanoworld.org.ru/data/01/data/avi/nanowrl1.gif

Подробности для любознательных: http://nanoworld.org.ru/post/51199/#p51199

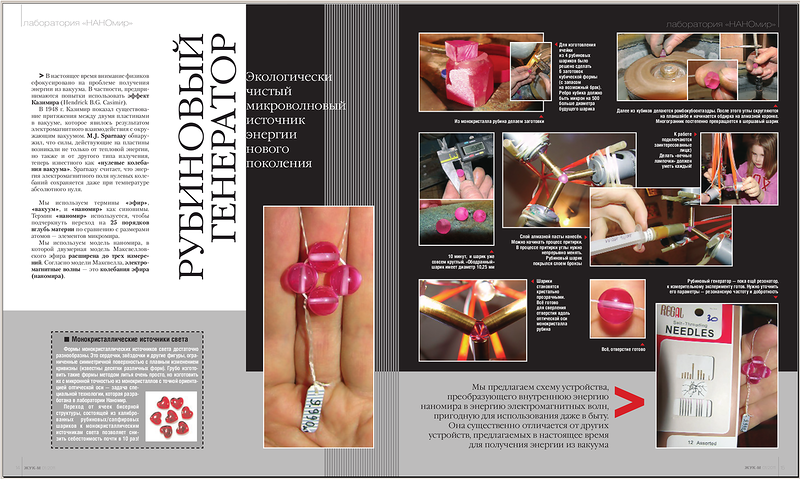
Области применения.

Рубиновый генератор может использоваться для освещения, обогрева, выработки электроэнергии. Он может обеспечить жилое или производственное помещение светом, теплом и электричеством.

Научнопопулярный фильм “Путешествие в Наномир”: https://www.youtube.com/watch?v=75tPH3vcDL4

Идея родилась одновременно с испытанием Emdrive в 1992 году.

 

http://img-fotki.yandex.ru/get/5819/158289418.19d/0_fec91_d028a2c3_XL.gif
Сегодня разработан ещё более эффективный Ruby Emdrive. Он сможет поднять в 1000 раз больше своего веса на Земле. На базе Ruby Emdrive можно делать летательные браслеты. Летать на них можно будет так же легко, как на флайборде.

https://img-fotki.yandex.ru/get/196161/158289418.3a2/0_16b039_f5777749_XL.jpg

Почему нас не финансируют из государственного бюджета?

В 1992-ом году Александр Кушелев испытал электромагнитный двигатель, не отбрасыващий реактивную струю. Прошло 22 года. Аналогичный двигатель (Microwave Engine, Emdrive) испытали в NASA. В 2017-ом его уже планируют испытывать в США на околоземной орбите. В России это, вероятно, не нужно. На наше письмо в Роскосмос никто не ответил.
В настоящее время проблема заключается в том, чтобы включить первый рубиновый генератор. Удобнее это сделать от импульсного магнетрона.

http://img-fotki.yandex.ru/get/9300/158289418.b7/0_b1d3d_8105a720_orig.jpg

На какой стадии проект в данный момент?

Созданы элементы будущего генератора и испытаны в рабочих условиях.

http://img-fotki.yandex.ru/get/5505/nanoworld.21a/0_51fbc_2faaf080_orig.jpg

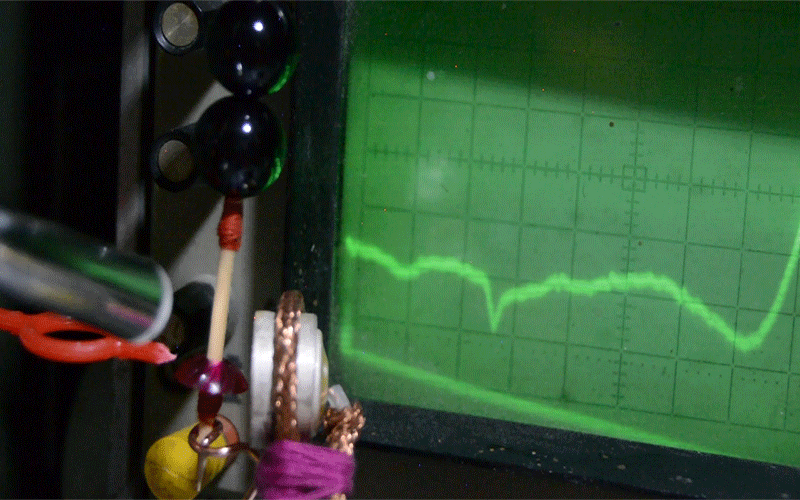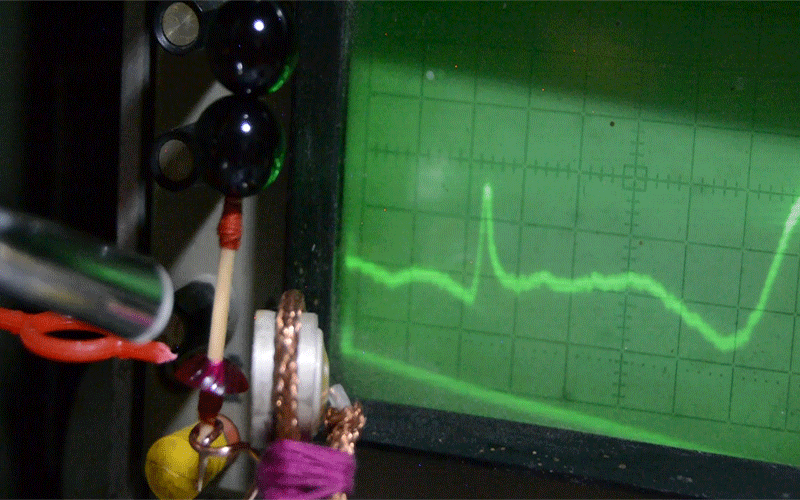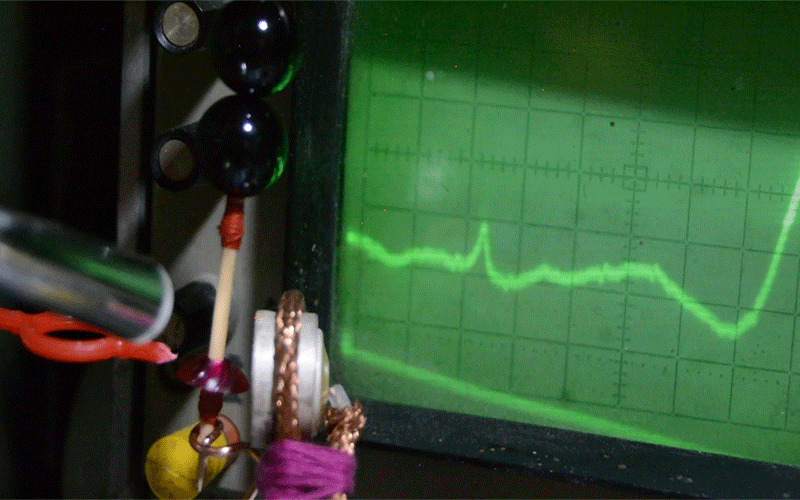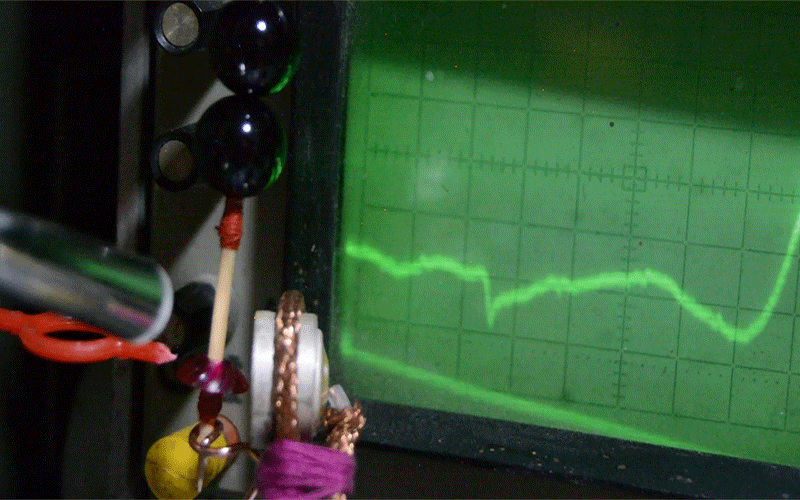
На фотографии - измерение параметров резонансной системы из рубина. Погрешность диаметров меньше микрона. Это и есть будущий источник энергии на 10 киловатт непрерывной мощности.

В Дубне был проведен эксперимент, на котором проверена защита от перенапряжения, т.е. элемент будущего генератора не сгорел, а “скинул” лишнюю энергию в виде свечения.

http://img-fotki.yandex.ru/get/9067/158289418.af/0_ae264_4777e0aa_orig.gif

Чтобы включить рубиновый генератор, нужно так же возбудить, но уже не один, а 4 шарика, образующих трансформатор внутренней энергии эфира.
Получено свечение сапфирового элемента в микроволновке.

На данный момент мы имеем практическое и теоретическое обоснование возможности включения такого генератора.

Нам не хватает только магнетрона с блоком управления для включения рубинового генератора. Деньги собираются на аренду этого оборудования и изготовление опытной партии рубиновых источников энергии. Инвесторы получат их в первую очередь. Для остальных будет изготовлена следующая партия рубиновых генераторов.

 Обсуждение

 Моделируем бифилярный фрактал...

Напомню, что объект может быть фракталом в одном измерении (по вертикали), но антифракталом в других измерениях (по горизонтали). А это значит, что в целом объект может быть "нормальным", т.е. не фрактальным и не антифрактальным. На первый взгляд кажется, что кроме игры слов тут ничего нет, но не торопитесь с выводами...

Введём понятие "степень фрактализации". Для фракталов она будет положительна, а для антифракталов - отрицательна. Если же по одним степеням свободы система является фракталом, а по другим - антифракталом, то может получиться компенсация степени фрактализации, и объект окажется "нормальным", хотя в действительности по одной координате он - фрактал, а по другим - антифрактал.

Эти слова обретают физический смысл, если мы начнём измерять некоторые параметры объектов, например, реактивное сопротивление.

Если фрактальный резонатор обладает реактивным сопротивлением, то его антипод может обладать емкостным сопротивлением. Если же свести в один объект фрактал и антифрактал, то реактивное сопротивление фрактала может компенсироваться емкостным сопротивлением антифрактала. В этом случае мы можем сделать "безинерционный" трансформатор внутренней энергии эфира, которым, вероятно, и является "ступенчатая пирамида", например, мегалитический комплекс Боробудур:

 

Мы начнём моделирование с более простого фрактала: 

 

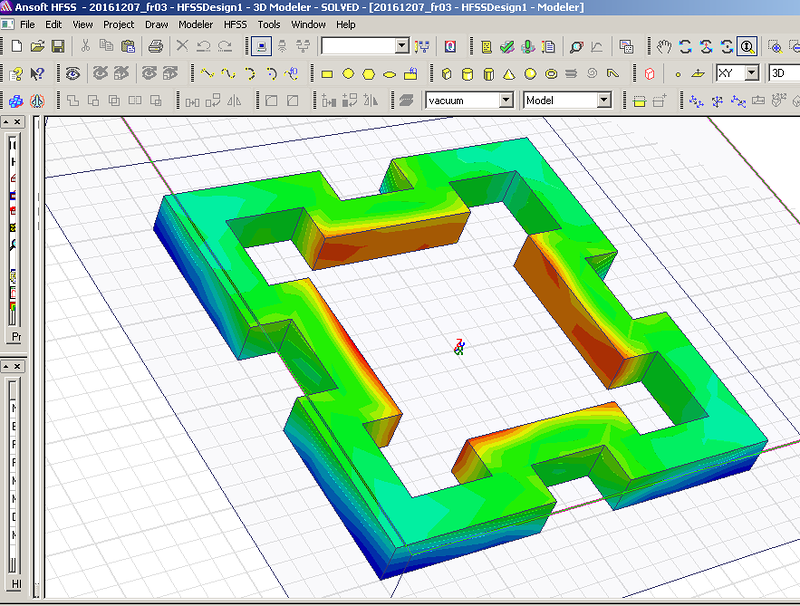
https://img-fotki.yandex.ru/get/52765/158289418.3a1/0_16af6c_91d3da69_XL.png
1.4 ГГц
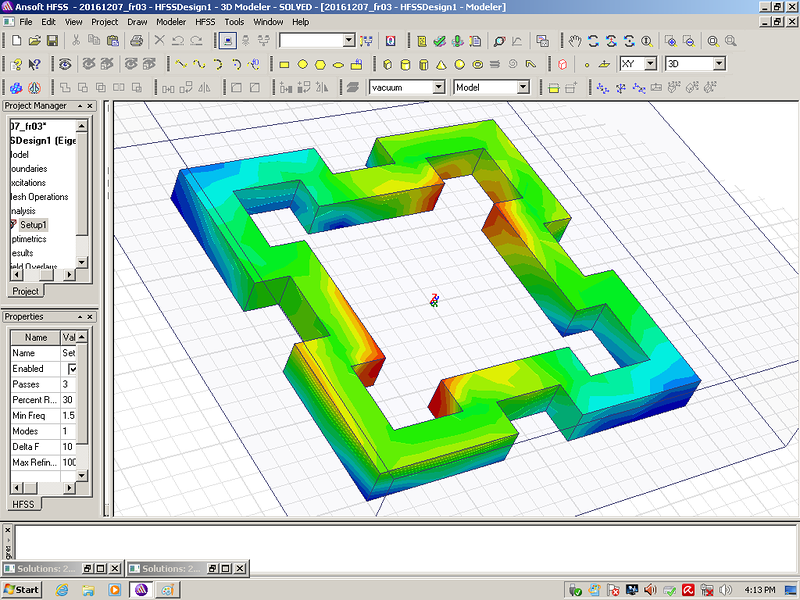
https://img-fotki.yandex.ru/get/118982/158289418.3a1/0_16af6d_1e617a1a_XL.png
2.12 ГГц
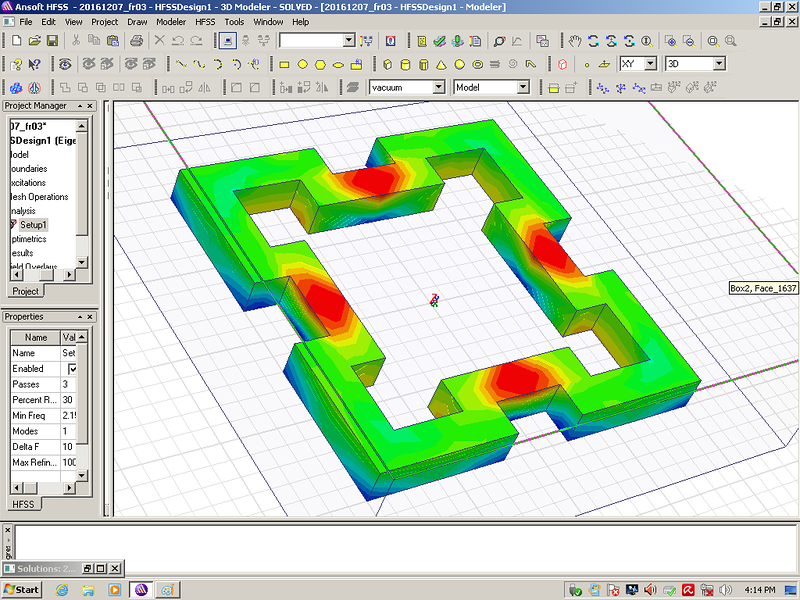
https://img-fotki.yandex.ru/get/118982/158289418.3a1/0_16af6f_77a21bf5_XL.png
2.579 ГГц
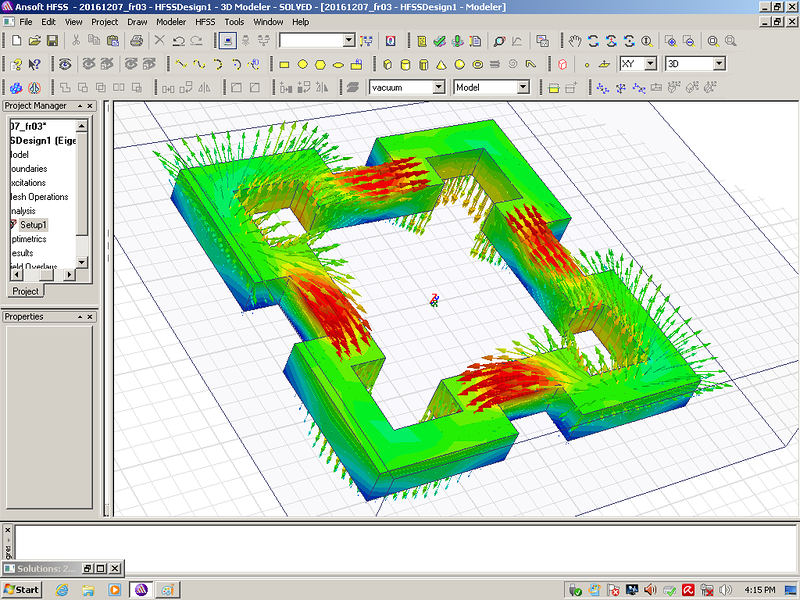
https://img-fotki.yandex.ru/get/171750/158289418.3a2/0_16af73_37280a98_XL.png
2.579 ГГц
https://img-fotki.yandex.ru/get/195419/158289418.3a2/0_16af6e_6a455bdc_XL.gif
2.579 ГГц
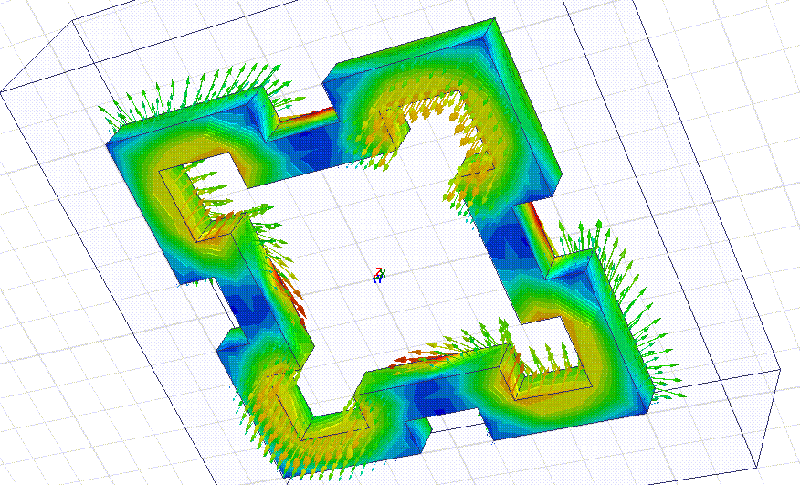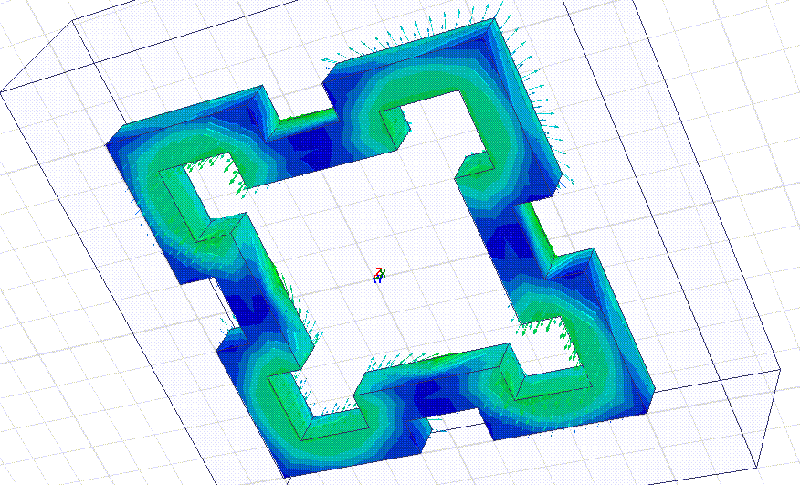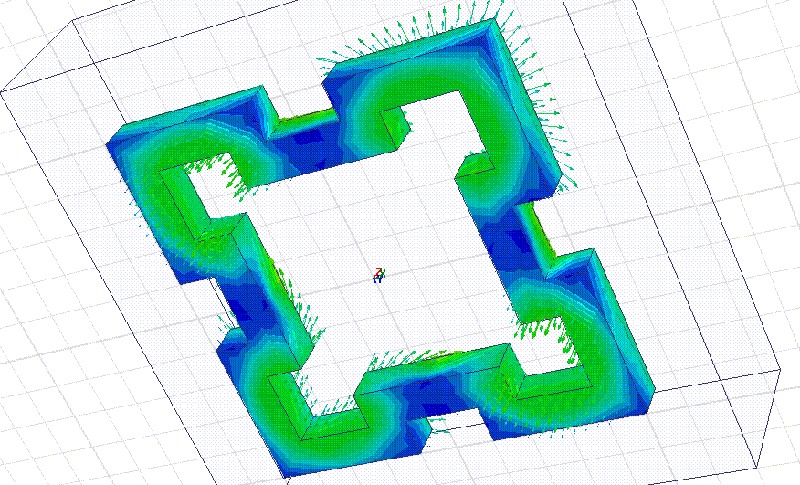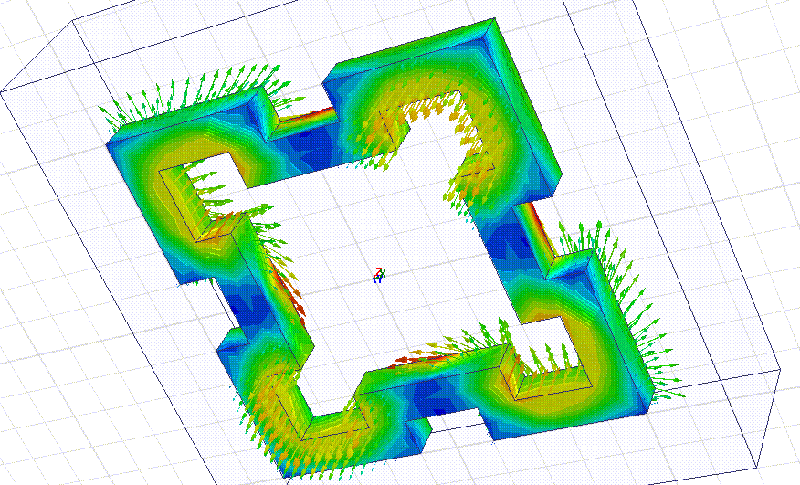
https://img-fotki.yandex.ru/get/198569/158289418.3a2/0_16af70_a34e259c_XL.gif
2.579 ГГц
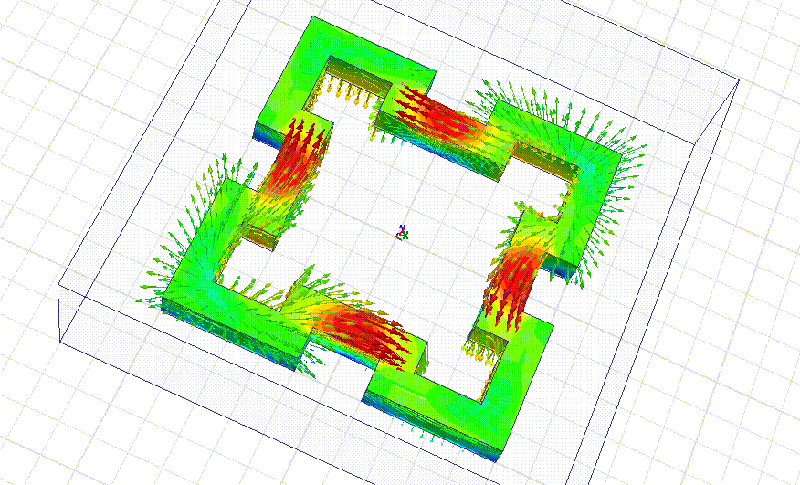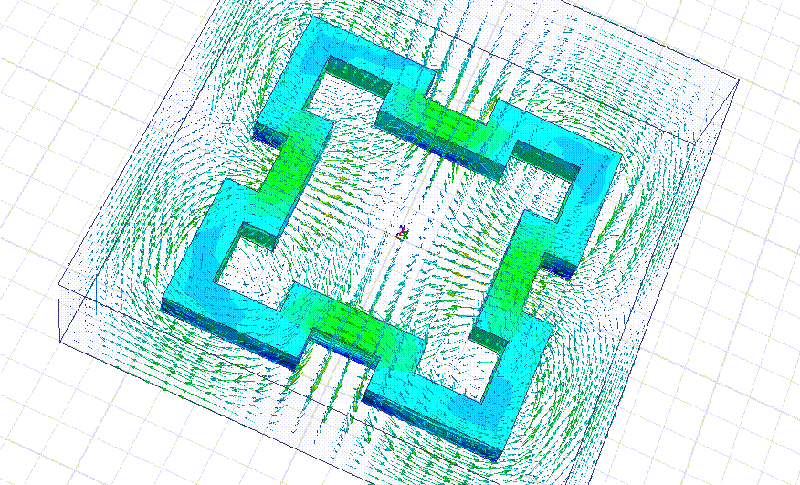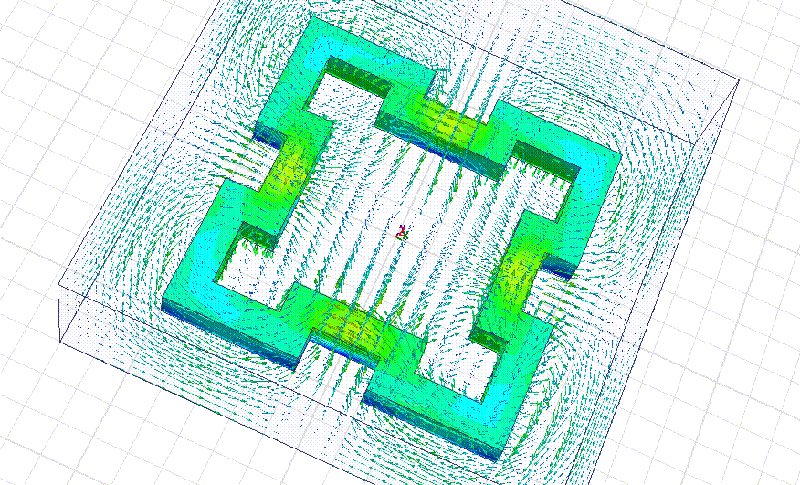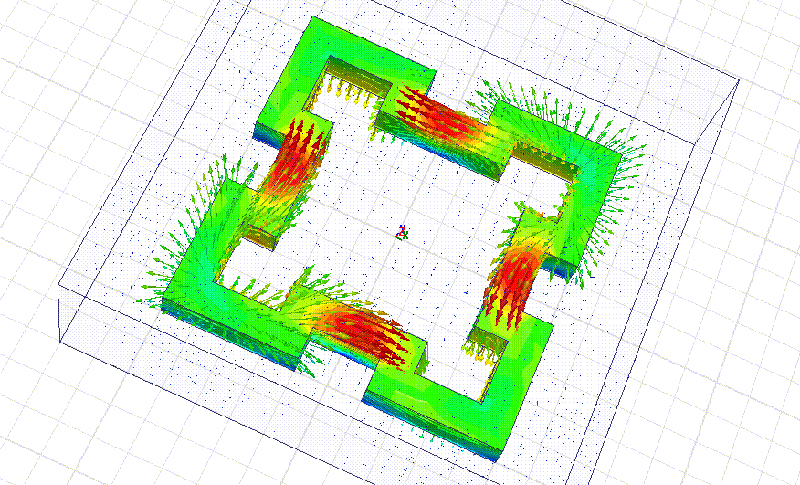
https://img-fotki.yandex.ru/get/169883/158289418.3a2/0_16af71_a944670d_XL.gif
2.579 ГГц
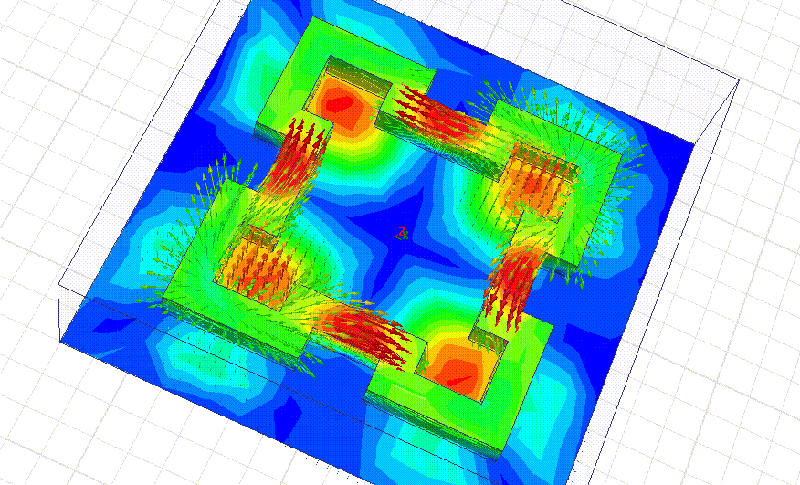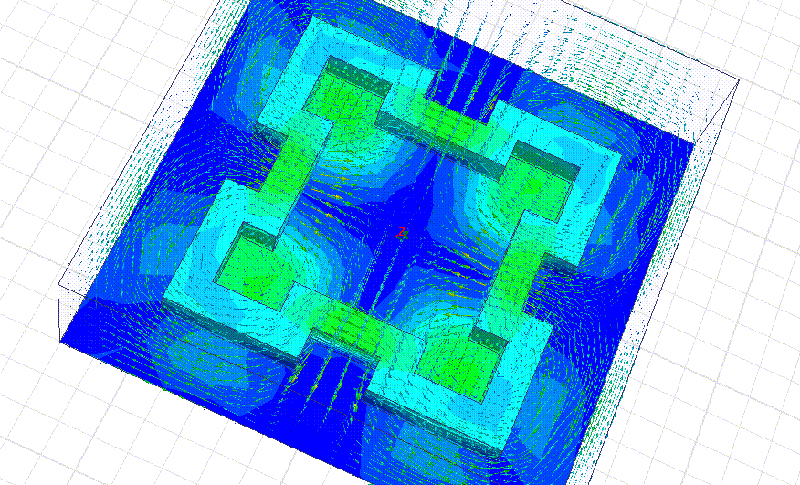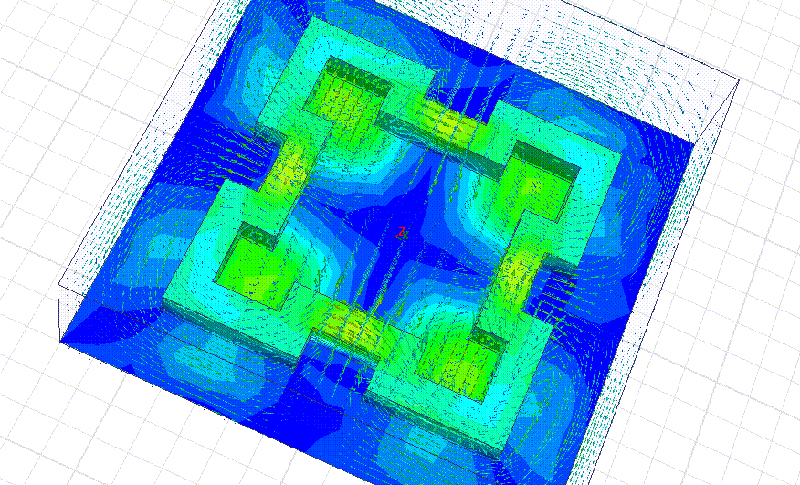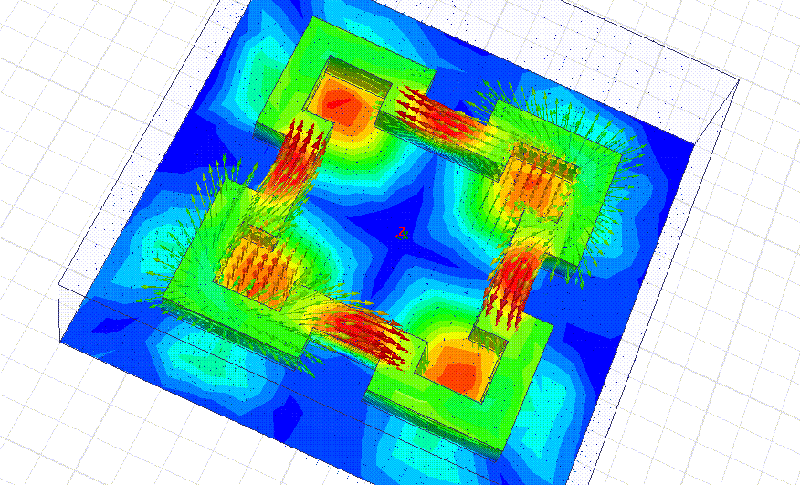
https://img-fotki.yandex.ru/get/197852/158289418.3a2/0_16af72_62c09b2d_XL.gif
2.579 ГГц

Сечение фрактала 10 мм. Материал рубин. Все размеры кратны 10 мм.

На примере этого фрактала мы видим, что рабочая частота действительно в несколько раз выше, чем у квадратного резонатора с теми же габаритными размерами. Добавление фрактальных уровней позволит повышать частоту в несколько раз на каждом фрактальном уровне!

 Обсуждение

 Мегалитический комплекс непарнозубых

https://img-fotki.yandex.ru/get/117474/158289418.3a1/0_16af03_dbbcc2ed_XL.jpg

Храм Прамбанан тоже имеет антифрактальную проекцию, т.е. "вывернутый назинанку квадрат Кантора". Интересно будет проверить резонансные свойства подобных бифилярных фракталов... 

 https://img-fotki.yandex.ru/get/51236/158289418.3a1/0_16af07_cbafd8c6_XL.jpg 

Обратите внимание на нечётное число зубов верхней челюсти 

 

 https://img-fotki.yandex.ru/get/197923/158289418.3a1/0_16af32_15ec77f1_XL.jpg

 Мегалитический комплекс Prambanan на острове Ява строили непарнозубые, которые изображали непарнозубых разных видов со своей планеты.

 https://img-fotki.yandex.ru/get/43800/158289418.3a1/0_16af04_e5647098_XL.jpg

Любопытный "гранёный банан" smile

https://img-fotki.yandex.ru/get/196486/158289418.3a1/0_16af05_f903f364_XL.jpg

Не совсем обычная лестница. И перила переменной высоты, и ступени, похоже не совсем по прямой идут...

 

https://img-fotki.yandex.ru/get/51057/158289418.3a1/0_16af06_aeedd75d_XL.jpg

 https://img-fotki.yandex.ru/get/53993/158289418.3a1/0_16af09_dff4b4d5_XL.jpg

Похоже, что эти штуковины работали на 5-ой или 6-ой колебательной моде...

https://img-fotki.yandex.ru/get/198998/158289418.3a1/0_16af0a_41df4bbd_XL.jpg

На шестой.

 

https://img-fotki.yandex.ru/get/62701/158289418.3a1/0_16af0b_ffa58bdd_XL.jpg
И на восьмой...

 Обсуждение

 Планета непарнозубых

Пополняем коллекцию непарнозубых

 https://img-fotki.yandex.ru/get/195132/158289418.3a1/0_16af33_49fc159_XL.jpg

Лаос, Вьентьян https://img-fotki.yandex.ru/get/165720/158289418.3a1/0_16af4e_ce2e6fb6_XL.jpg

https://img-fotki.yandex.ru/get/198488/158289418.3a1/0_16af54_f610dcf2_XL.jpg 

https://img-fotki.yandex.ru/get/194492/158289418.3a1/0_16af56_e4ea686e_XL.jpg 

https://img-fotki.yandex.ru/get/195431/158289418.3a1/0_16af59_4482c69e_XL.jpg

https://img-fotki.yandex.ru/get/198613/158289418.3a1/0_16af5a_9dcfdd4d_XL.jpg

https://img-fotki.yandex.ru/get/195637/158289418.3a1/0_16af5b_89542db0_XL.jpghttps://img-fotki.yandex.ru/get/198026/158289418.3a1/0_16af5d_dada9dfe_XL.jpghttps://img-fotki.yandex.ru/get/198569/158289418.3a1/0_16af5c_cccf4be_XL.jpg

 https://img-fotki.yandex.ru/get/104083/158289418.3a1/0_16af5e_3417d9f1_XL.jpg

https://img-fotki.yandex.ru/get/195786/158289418.3a1/0_16af5f_63b7150d_XL.jpghttps://img-fotki.yandex.ru/get/198026/158289418.3a1/0_16af61_a2fca92a_XL.jpghttps://img-fotki.yandex.ru/get/197213/158289418.3a1/0_16af60_66e1b29c_XL.jpghttps://img-fotki.yandex.ru/get/94189/158289418.3a2/0_16b066_3ba4bb91_XL.jpghttps://img-fotki.yandex.ru/get/195518/158289418.3a2/0_16b071_5aa7edd2_XL.jpg

https://img-fotki.yandex.ru/get/198017/158289418.3a1/0_16af62_1b01926a_XL.jpg

 

 https://img-fotki.yandex.ru/get/195132/158289418.3a2/0_16b067_c2075856_XL.jpg

 

https://img-fotki.yandex.ru/get/196020/158289418.3a2/0_16b068_fdc420b7_XL.jpg
А это похоже маска непарночелюстного, т.е. у него три верхних челюсти... Или две 

 https://img-fotki.yandex.ru/get/194989/158289418.3a2/0_16b069_ac0cf875_XL.jpg

Много зубов не нужно. Особенно если это - сменные насадки, как у кухонного комбайна.

https://img-fotki.yandex.ru/get/27200/158289418.3a2/0_16b06a_c9983e9d_XL.jpg

Трёх зубов между клыками вполне достаточно "для полного счастья" smile 

 https://img-fotki.yandex.ru/get/195419/158289418.3a2/0_16b06b_4621047_XL.jpg

Количество зубов не так критично, как количество элементов источника энергии, защищающих череп.

 https://img-fotki.yandex.ru/get/194425/158289418.3a2/0_16b06c_363799d8_XL.jpg

Три зуба между клыками - устойчивый инопланетный генотип...

https://img-fotki.yandex.ru/get/6440/158289418.3a2/0_16b06d_cacb7e6d_XL.jpg 

https://img-fotki.yandex.ru/get/103213/158289418.3a2/0_16b06e_a5eaba90_XL.jpg

Пять зубов между клыками - тоже устойчивый инопланетный генотип.

https://img-fotki.yandex.ru/get/169883/158289418.3a2/0_16b06f_7de220df_XL.jpg

Скорее всего непарнозубые с тремя и с пятью зубами между клыками прилетели с разных звёздных систем.

https://img-fotki.yandex.ru/get/196142/158289418.3a2/0_16b070_7d9b7f0f_XL.jpg

На нижней челюсти крупные зубы, а на верхней мелкие? Или там не зубы, а одна пластина?

 

https://img-fotki.yandex.ru/get/196631/158289418.3a2/0_16b072_cb30b458_XL.jpg
Тут уже непонятно, то ли непарнозубый, то ли непарноклювый... 

https://img-fotki.yandex.ru/get/196631/158289418.3a2/0_16b073_8089b478_XL.jpg

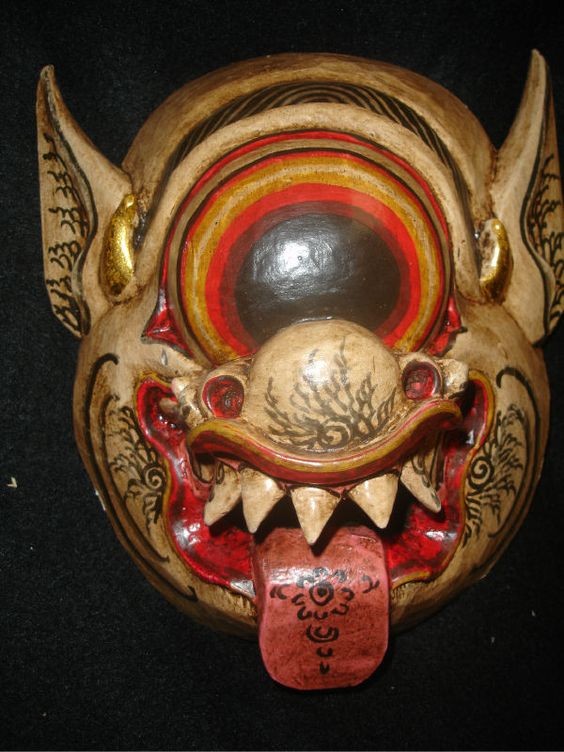
 https://img-fotki.yandex.ru/get/101645/158289418.3a2/0_16b076_7d27445d_XL.jpg

Залетали на остров Бали и непарнозубые циклопы...

https://img-fotki.yandex.ru/get/198569/158289418.3a2/0_16b077_1f91e289_XL.jpg

Когда треугольные зубы входят со смещением, то в одной челюсти их должно быть чётное число, а в другой - нечётное. Ещё один тип непарнозубых... 

https://img-fotki.yandex.ru/get/173476/158289418.3a2/0_16b078_85fe8d38_XL.jpg

В Африке тоже видели непарнозубых

https://img-fotki.yandex.ru/get/196070/158289418.3a2/0_16b079_e4f8d5de_XL.jpg
Как изобразить нечётное число зубов, если у Вас чётное число зубов?

Очень просто! Нарисовать зубы на губах smile 

https://img-fotki.yandex.ru/get/196010/158289418.3a2/0_16b07a_4001295b_XL.jpg

И здесь мы видим непарнозубых... 

Можно уже писать дисер на тему: "Распространённость непарнозубых в видимой части Вселенной" smile

https://img-fotki.yandex.ru/get/197807/158289418.3a2/0_16b0cb_c28fa552_XL.jpg
Враги этого непарнозубого были ... парнозубыми!

https://img-fotki.yandex.ru/get/197102/158289418.3a2/0_16b0d0_c75bc337_XL.jpg

Как вам инопланетная "сладкая парочка"?

https://img-fotki.yandex.ru/get/98619/158289418.3a2/0_16b0d1_da9eb28_XL.jpg

Непарнозубый, зато парноносый!

https://img-fotki.yandex.ru/get/169451/158289418.3a2/0_16b0d2_57403429_XL.gif

У этого непарнозубого ещё что-то непарное...

https://img-fotki.yandex.ru/get/42925/158289418.3a2/0_16b0d3_3b03eca3_XL.jpg

https://img-fotki.yandex.ru/get/105020/158289418.3a2/0_16b0d6_9cecabe6_XL.jpg

https://img-fotki.yandex.ru/get/99813/158289418.3a2/0_16b0d7_bac6f787_XL.jpg

Бывают непарнозубые враги непарнозубых и парнозубые враги парнозубых... 

 https://img-fotki.yandex.ru/get/170815/158289418.3a2/0_16b0d8_89133399_XL.jpg

С зубами всё ясно, но что у него с носом?!

https://img-fotki.yandex.ru/get/177849/158289418.3a3/0_16b0d9_347b39a5_XL.jpg

Непарнозубый круглозубец smile

https://img-fotki.yandex.ru/get/194425/158289418.3a3/0_16b0da_c70b0138_XL.jpg

А сколько зубов у этого непарноглазого, за хоботом не видно...

https://img-fotki.yandex.ru/get/195518/158289418.3a3/0_16b0db_f7107445_XL.jpg

Непарноглазые чаще бывают непарнозубыми. Кстати, в оригинале он мог быть весь запломбирован нефритом... 

https://img-fotki.yandex.ru/get/196600/158289418.3a3/0_16b0dc_fd43e468_XL.jpg

Ещё один непарноглазый непарнозуб...

https://img-fotki.yandex.ru/get/194550/158289418.3a3/0_16b0de_daf7eecd_XL.jpg

https://img-fotki.yandex.ru/get/45704/158289418.3a3/0_16b0df_3ecb3b78_XL.jpg

Непарнозубые скелеты... 

https://img-fotki.yandex.ru/get/45704/158289418.3a3/0_16b0e2_1802ccc4_XL.jpg

Непарноглазый непарнозуб

https://img-fotki.yandex.ru/get/174352/158289418.3a3/0_16b0e3_a6ccb1e2_XL.jpg

Трехглазая инопланетная мордашка из Непала... 

https://img-fotki.yandex.ru/get/195419/158289418.3a3/0_16b0e4_5433a0ea_XL.jpg

Непарноглазый непарнозуб

Обсуждение

 Жилет-катафот трехглазых

 https://img-fotki.yandex.ru/get/107080/158289418.3a3/0_16b112_a005ba04_XL.jpg

Очень реалистично выглядит скульптура этого непарноглазого инопланетянина. Фальшивые лица видны и на груди, и на животе, причём "вверх тормашками" :) На шее висит ожерелье сменных фальшивых голов. Голова может быть защищена металлическим шлемом. При этом глаза могут быть защищены алмазными фильтрами со светозащитным покрытием, за которым могут быть расположены усилители ослабленного оптического сигнала.

https://img-fotki.yandex.ru/get/46114/158289418.3a2/0_16b0cc_a2e992d2_XL.jpg

А у этого за головой вообще ... квадроваджра (не путать с квадрокоптером!)

 Обсуждение

Уважаемые коллеги! Все, кто помогает создавать пикотехнологию, рубиновую энергетику, поднимает нашу цивилизацию на новую ступень развития. Всех нас можно поздравить с крупным успехом. Эксперименты в США, Германии и в Израиле подтвердили, что мы находимся на верном пути по трём главным научным направлениям лаборатории Наномир.

По теме "Рубиновая/микроволновая энергетика и транспорт" осталось сделать последний шаг, включить готовые источники энергии. Конечно, с помощью магнетрона миллиметрового диапазона создать рубиновую энергетику можно за считанные дни, но для этого нужно доделать номинальный ряд эллипсоидов и рубиновый энергетический конструктор.

Спасибо за поддержку! 

 

Что нужно лаборатории для ближайших исследований:

Skype, 2016-04-25:

[12:51:45] Jocie Lee: Now we have round shape . the maximum size is 11mm

 

 

[13:26:01] Jocie Lee: The price is 773 usd/pcs

[13:30:11] Кушелев Александр Юрьевич: Thank You very mach!

[13:31:24] Кушелев Александр Юрьевич: Do You have diamond box (color, for example yellow) 4x4x1mm ? If Yes, need price... 

[13:33:50] Кушелев Александр Юрьевич: And I need this forms:

  

[13:59:46] Jocie Lee: oh...I am sorry. We dont sell box

[14:02:33] Кушелев Александр Юрьевич: OK! I wait money from my investors. I need 773usd/pcs diamond.

[14:02:49] Jocie Lee: OK

[14:03:13] Кушелев Александр Юрьевич: Do You make color diamonds?

[14:04:50] Jocie Lee: I think this colorful stone is cubic zirconia

[14:05:23] Кушелев Александр Юрьевич: But I need color synthetic diamonds for science experiments :)

[14:06:50] Кушелев Александр Юрьевич: I have cubic zirconia, but it has bad electromagnetic parameters. I need color synthetic diamond only. Your diamond size is very good!

1. Заказать алмазный энергетический конструктор. Минимальный заказ 773 USD + EMS доставка. 

2. Оплатить покупку или аренду измерительной аппаратуры на диапазон от 4 до 32 ГГц. (От $1000). Идеальный вариант: http://www.keysight.com/en/pd-460865-pn-E8257D/psg-analog-signal-generator?&cc=RU&lc=rus

3. Начать третий этап создания средства для продления жизни: http://nanoworld.org.ru/topic/818/

Книга "Пикотехнология белков" уже в продаже!

Подробности

Менеджеры, которые найдут заказы на структуры белков, получат 80% от суммы заказа! 

 Приглашение к сотрудничеству

Лаборатория "Наномир" готова к взаимовыгодному сотрудничеству. 

В одиночку внедрить технологии, выводящие цивилизацию на новый уровень,  невозможно. Благодаря поддержке множества заинтересованных людей проделана огромная работа. Ознакомиться с её результатами можно изучив материал рассылки "Новости лаборатории Наномир". Люди науки могут изучить научные труды.

Вклад каждого не останется незамеченным в случае успеха в реализации научных проектов. Результаты совместной деятельности принадлежат участникам проекта пропорционально коэффициентам творческого и финансового участия.

Основные разработки: 

 Микроволновый источник энергии

Работы по созданию новой энергетики (микроволновой) ведутся с 1992 года.

В 2011 году были куплены рубиновые шарики для эксперимента на сумму ~1000 долл. Был проведен первый эксперимент в Дубне. В результате было сделано научное открытие, проверена защита диэлектрических резонаторов от перенапряжения. В марте 2016 года проведен первый этап эксперимента в микроволновой печи. Цель эксперимента - включение рубинового генератора. На первом этапе удалось возбудить рубиновый резонатор до уровня поверхностного пробоя, т.е. до напряжённости 1000 000 вольт на метр. Цель следующего этапа - заставить рубин светиться.

 

 

Для завершающего этапа исследований по созданию микроволновой энергетики не хватает номинального ряда рубиновых резонаторов, который может быть изготовлен на китайской фабрике. Это стоит на порядок дешевле, чем качественная измерительная аппаратура миллиметрового диапазона.

  "Регенерация репродуктивного возраста"

28 сентября 2011г. в Институте геронтологии (г.Киев) начался эксперимент по созданию "Регенератора репродуктивного возраста". В 2012-ом году мы уже знали, как омолодить лабораторных животных. Это было описано в 281-ом выпуске рассылки "Новости лаборатории Наномир. "Прожиточный минимум вампира"

В 2014-ом году американские ученые смогли реализовать этот вариант омоложения. Тем не менее мы ещё можем успеть первыми создать дешевый регенератор, возвращающий молодость, но для этого необходимо закупить праймеры для идентификации сигналов отключения феноптоза (механизма старения), как это делает эмбрион во время беременности. Если омоложение по-американски обойдётся заказчику в 250-500 долл. ежедневно, то дешёвый вариант омоложения будет стоить всего 20-30 копеек в день.

Программа исследований Презентация Обсуждение

  Пикотехнология 

Созданы первые версии пикотехнологии (выпуски рассылки 212 270 271 272 ), с помощью которой Александр Кушелев и Виктория Соколик сделали более10 научных открытий. Подготовлена к печати монография "Пикотехнология белков".

Виктория Соколик: Уважаемые коллеги, Вашему вниманию предоставляется услуга -- моделирование 2D и 3D структуры любого белка без ограничений в его размере и степени изученности с помощью программного обеспечения, базирующемся на принципиально новом подходе декодирования нуклеотидной последовательности, детерминирующей данный белок.

Всё, что необходимо от заказчика, это нуклеотидная последовательность мРНК интересующего его белка (или код этой нуклеотидной последовательности в EMBL, или хотя бы код самого белка в PDB).

В течение 1-3 суток мы готовы предоставить Вам схему вторичной структуры заказанного белка (2D), модель его пространственной структуры (3D) в виртуальном пространстве, а также файл .pdb с координатами каждого атома белка. 

Файл .pdb может быть использован по аналогии с файлами закристаллизованных белков из PDB банка для дальнейшего конформационного анализа белка методами молекулярной динамики с учётом физико-химической специфики микроокружения белка или его взаимодействия с лигандами.

Таким образом, Вы сможете максимально быстро удобным для Вас способом (по электронной почте, на сайте либо на электронном носителе) получить информацию о структурном шаблоне Вашего белка.

Определены две структуры белка (пробный заказ) для Испанского заказчика.

В книге "Пикотехнология белков" приведены примеры 100 белковых структур. 

Цена  заказов -- договорная. 

 Сотрудничество может быть различным:

- участие в научных дискуссиях на форуме (конструктивное)

- совместное создание коммерческого продукта

- поиск инвесторов

- выступить менеджером по продаже готовых коммерческих продуктов 

- конструктивные предложения по продвижению идей лаборатории Наномир

- содействие в проведении экспериментов и т.п.

- написание совместных научных статей и т.п.

- материальный вклад (денежный или обеспечение оборудованием и материалами)

 

Пожалуйста, сообщайте о своем вкладе, чтобы мы зачли Вас как партнера лаборатории Наномир.

+7-926-5101703,   +7-903-2003424,  +7-916-8265031, Skype: Kushelev2009, mail: kushelev20120@yandex.ru

веб-мани: WM-кошелек R426964799301 Другие способы перевода