Выпуск 523
Лаборатория Наномир
Когда реальность открывает тайны,
уходят в тень и меркнут чудеса ...
3D-грани (дани) электромагнитного 4D-процессора
Что произойдёт, если расположить объёмные резонаторы рядом?
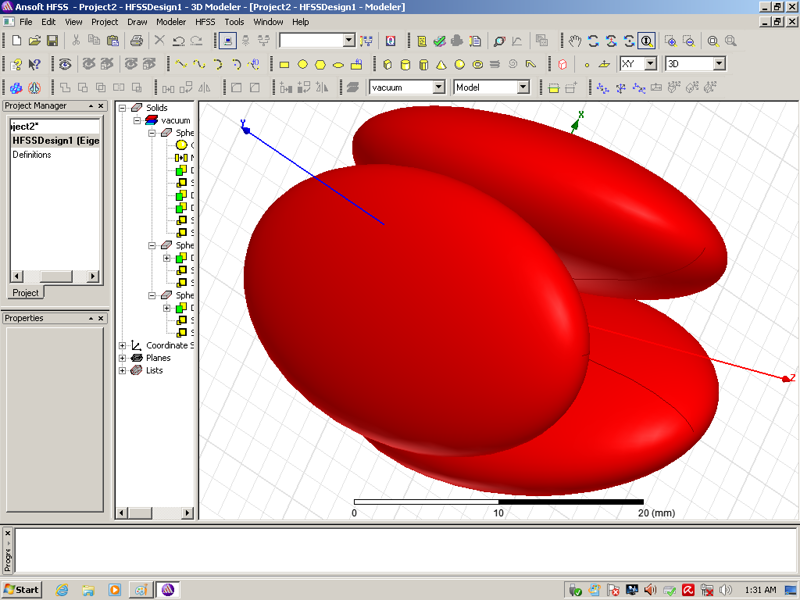
Если между ними возникнет связь, то они могут начать работать в другом, "коллективном" режиме.
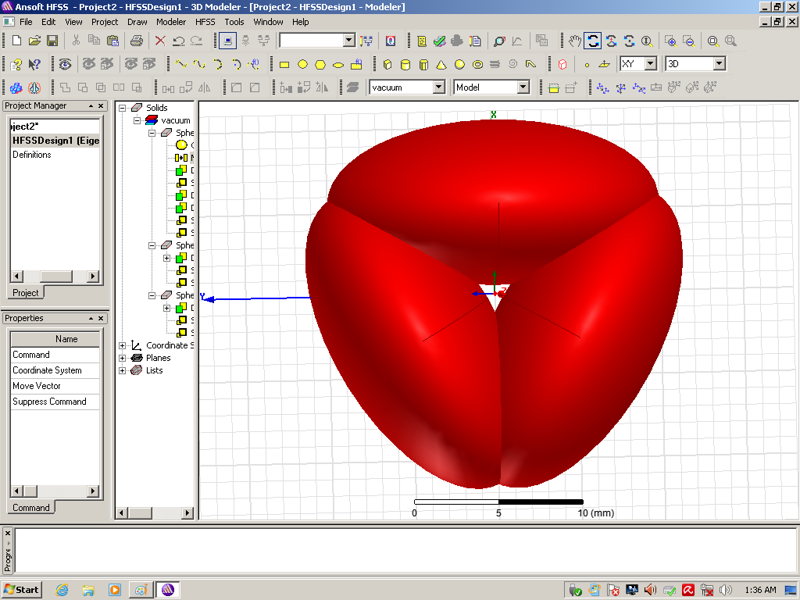
И этот "коллективный" режим можно сохранить в резонаторе, полученном объединением отдельных элементов в моноблок.


Понятно, что такую операцию можно проводить многократно, комбинируя объёмные грани (назовём их дани (от 3D-грани)) в фигуру, которую по аналогии с многогранником будем называть многоданником.



Гроздь является частным случаем многоданника.

Пример рёберного многоданника

Незамкнутый многоданник
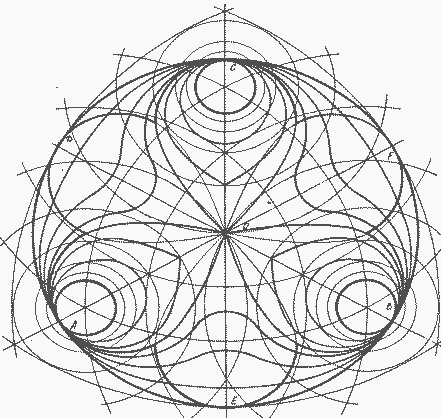
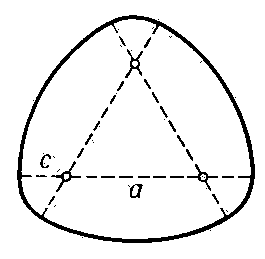
Триллипс-триллипсоид-многоданник Кушелева.



Цветок трилипс, три эллипсоида и триллипсоид
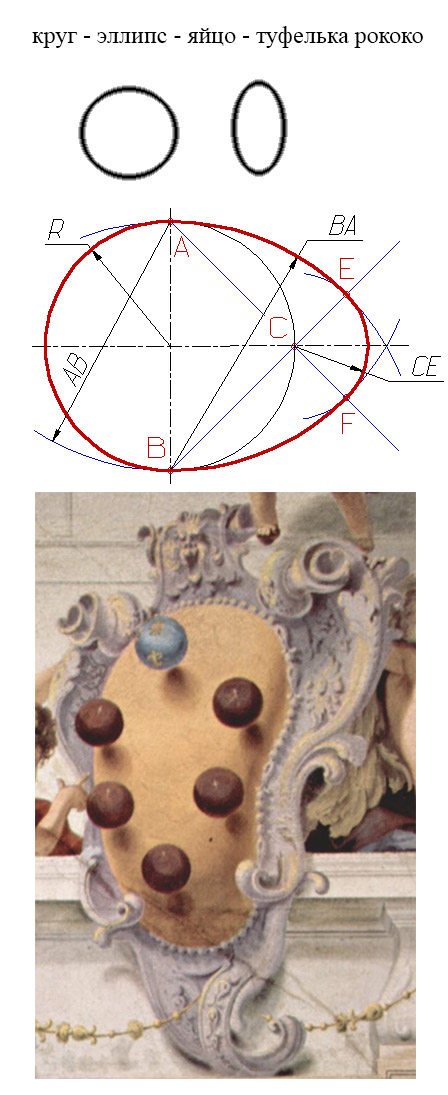
У окружности один центр. У эллипса - два фокуса. Можно изобразить фигуру с тремя фокусами (триллипс), четырьмя и более. На базе этих фигур можно построить объёмные фигуры: шар, эллипсоид, триллипсоид и т.д.
Является ли триллипс овалом / кривой Кассини?
Линиями Кассини называются геометрические места точек (М), для которых произведение расстояний (F1M x F2M = d), где (F1; F2) – фиксированные фокусы, (d) – постоянная.
Сравним с определениями эллипса / триллипса / поллипса:
Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) —геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек 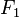 и
и 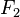 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
(называемых фокусами) постоянна и больше расстояния между фокусами, то есть
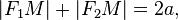 причём
причём 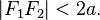
Триллипс - геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до трех данных точек F1, F2 и F3 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть F1M + F2M + F3M = 3a, причём FF < 3a
Поллипс - геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до N данных точек F1, F2 ... FN (называемых фокусами) постоянна и больше расстояния между фокусами, то есть F1M + F2M + ... FNM = Na, причём FF < Na
Тем не менее, триллипс и поллипсы - это, как выяснилось, просто овалы, простейшим из которых является эллипс.
Поллипс-поллипсоид.

Поллипсоид - оболочка многоданника.
В 522-ом выпуске рассылки мы уже обсуждали простейшие многоданники. В этот раз мы пойдём дальше. Какое количество фрактальных уровней может быть у многоданника? Теоретически - бесконечное. По крайней мере достаточно большое, чтобы это было трудно реализовать технически.

Галтованные многогранники представляют собой кривогранные фигуры, но в действительности являются многоданниками, формируя 3D-"грани" (дани) электромагнитного поля резонансной системы.

Размеры этих систем могут варьироваться от микроскопических (микроны) до космических (десятки тысяч км)
Изучая следы на полях, я обратил внимание на округлённые фракталы, которые обычно насчитывают не более 5 уровней. Вероятно, этого количества фрактальных уровней достаточно для получения высоких параметров фрактальных многоданников.

Типичный округленный фрактал насчитывает 4-5 фрактальных уровней.
Известны фрактальные системы, где на первый взгляд всего 2 фрактальных уровня. На самом деле это - иллюзия. Давайте посчитаем вместе.
1. Маленький эллипсоид.
2. Квадратная ячейка из маленьких эллипсоидов
3. Крупный эллипсоид из квадратных ячеек.
На самом деле есть ещё и 4-ый уровень. Мы уже знаем, что в эллипсоиде есть низкочастотная колебательная мода и высокочастотная. Это значит, что в ячейке эллипсоиды связаны через колебательную моду "шепчущей галереи" и в то же время могут работать на нижней резонансной частоте. В свою очередь ячейки, состоящии из маленьких эллипсоидов могут располагаться в пучностях стоячей волны (мода "шепчущей галереи") большого эллипсоида. Таким образом, электромагнитное поле структурировано четырьмя фрактальными уровнями, связанными между собой, как гармоники периодического несинусоидального сигнала. Какой формы сигнал может формировать резонансная система "Фрактальное яйцо"? Это зависит от кратности частот фрактальных уровней. В нюансах этой системы можно ещё долго разбираться, но главное, что уже удалось понять, это новый уровень геометрического представления, когда от плоских граней мы переходим к трёхмерным, четырехмерным и фрактальным "граням" высших порядков.
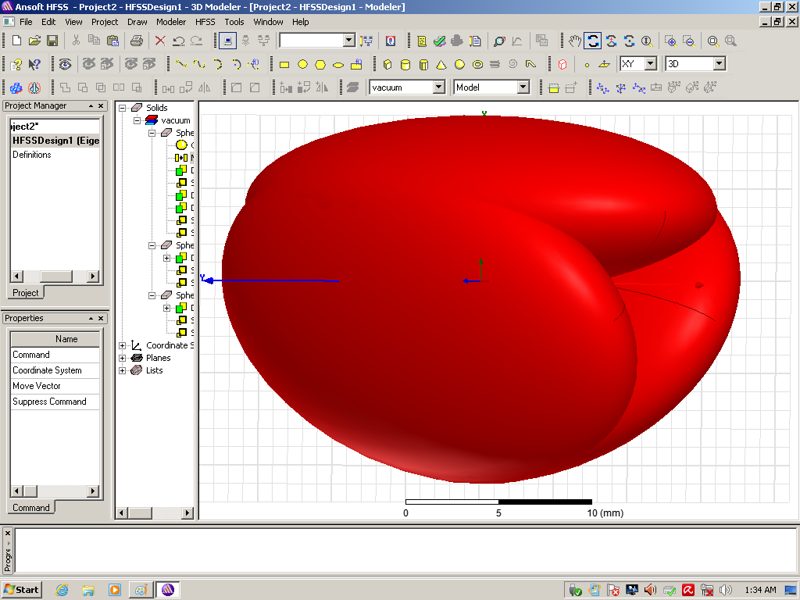
Фигура, образованная трехмерными "гранями" (данями) в свою очередь может рассматриваться уже как четырехмерная "грань".
В этом ключе можно рассматривать эволюцию электромагнитных процессоров: Три шарика - три эллипсоида - три морских камня - трёхданник Кушелева - трехгранное яйцо - трёхгранный спироид - "шишка"...



Семейство поверхностей для удержания даней. Понятно, что шишками эти формы можно назвать лишь условно...

Это сложные резонансные системы, многоданники, которые только похожи на шишки...
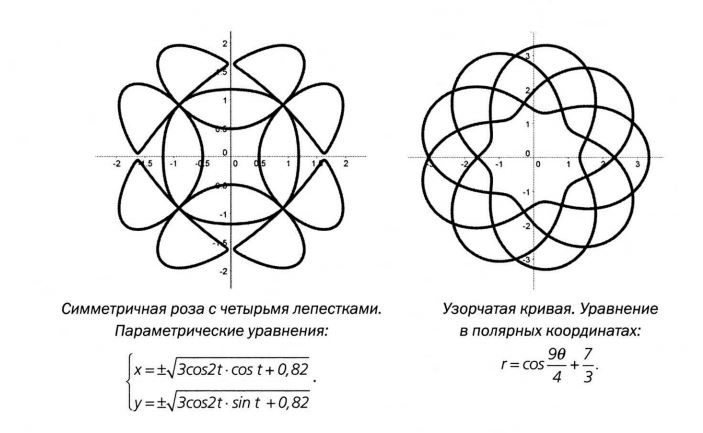
Объёмные фигуры могут строиться на основе плоских, хотя некоторые могут не иметь двухмерной основы...
Эллипс не шестеренка, но ...

Но существуют эллиптические шестеренки и звёздочки для велосипеда.
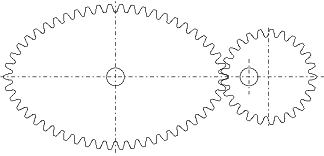
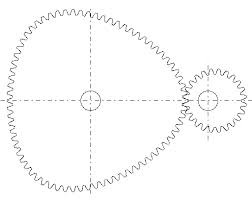
Эллипс и триллипс могут выполнять модулирующую функцию для шестеренок.


Это же относится и к поллипсам, хотя реальные модулирующие функции - циклоиды или овалы Кассини.

Это уже не эллиптические, а эллипсоидальные шестеренки. Если их изготовить из рубина, то мощность источника энергии может быть существенно выше, чем у сферической рубиновой шестеренки:
Моделируем африканский трёхданник.

Трехгранная призма этой африканской маски может копировать резонансную систему защиты от композитных лучей, "Африканский трехданник". Отверстие "пасть" прозрачна для излучения оптического диапазона, но непрозрачна для композитных лучей трезубцев / ваджр. Ионы начинают двигаться по кругу, а волны с длиной больше, чем сечение "пасти" отражаются. В маску может быть встроен перископ, позволяющий видеть глазами, которые находятся прямо за фальшивыми глазами, нарисованными на маске.
Модель одной дани этого африканского трёхданника у нас уже есть:
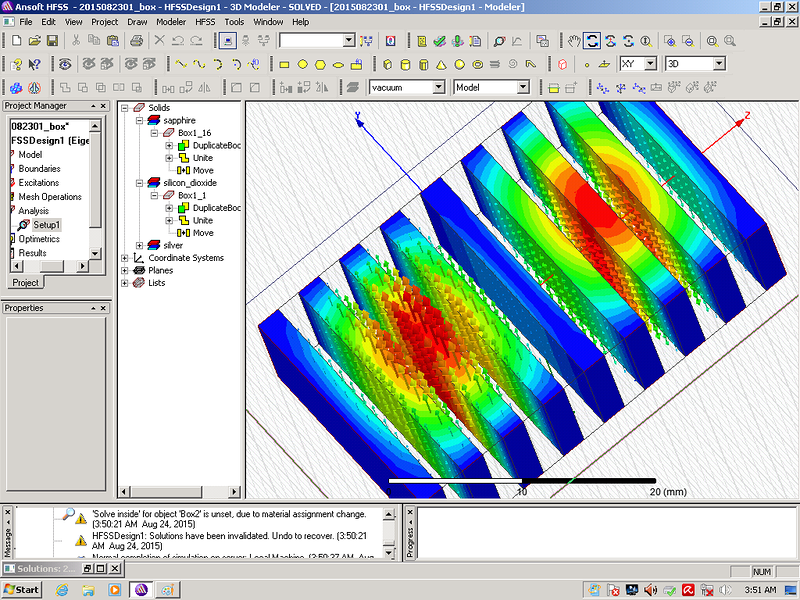
Как будут формироваться общее поле трёхданника, ещё предстоит выяснить в ближайшее время...
Ломогранники и ломоданники Кушелева
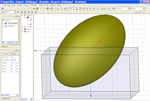
Грани и дани можно "ломать", т.е. делить на части и преобразовывать. Это позволяет, например, преобразовать источник энергии в двигатель.
Дэллипс, дэллипсоид Кушелева - содержательные сплайн-подмножества.
Зачем деформировать эллипс и эллипсоид? Деформированный эллипсоид, как выяснилось, создаёт дополнительные градиенты внутренней энергии эфира, что увеличивает мощность источника энергии / двигателя. При этом деформация должна быть правильной...
Группоиды - фигуры, в частности, многоданники, построенные на группах реперных точек.

Семейство поверхностей для удержания даней.

Располагая дани (объёмные "грани") по реперным точкам можно получить резонансную систему со свойствами, например, кварков или кварковых систем...
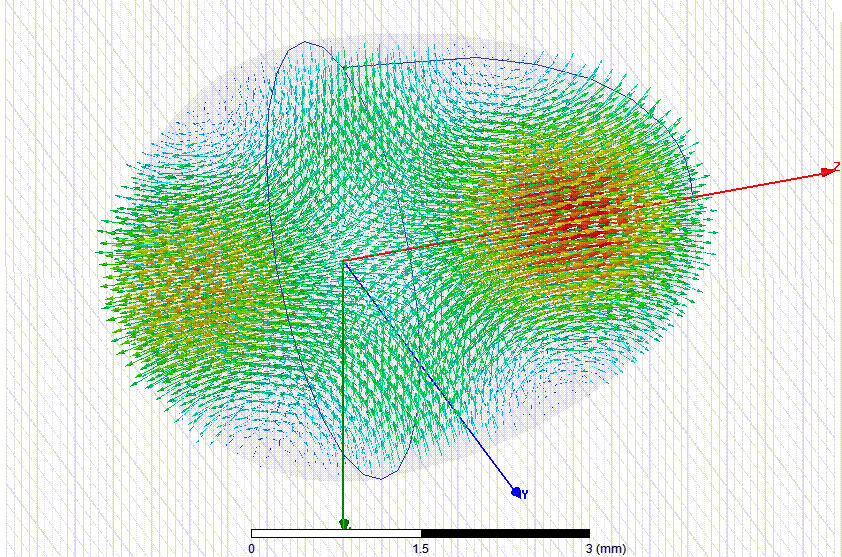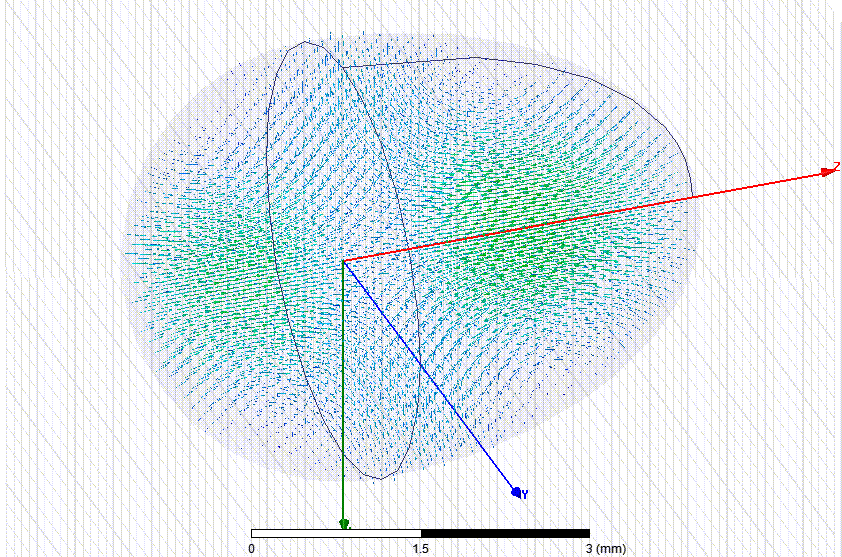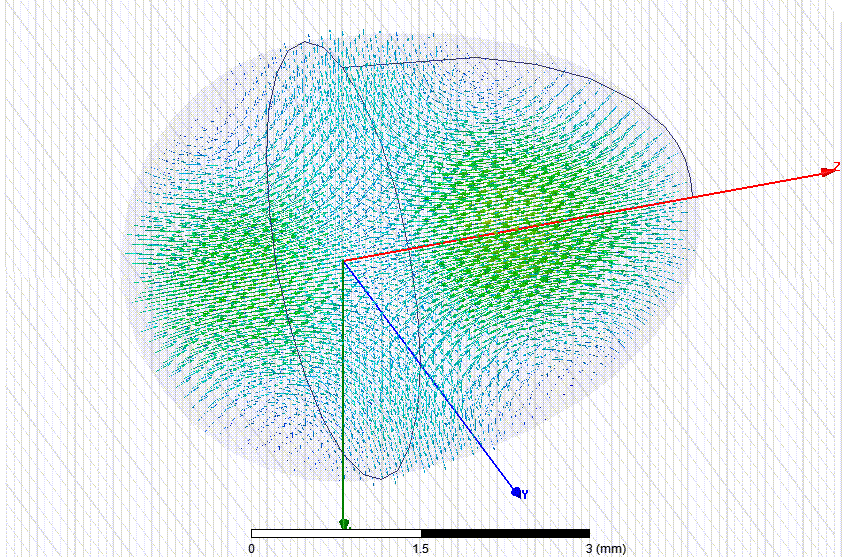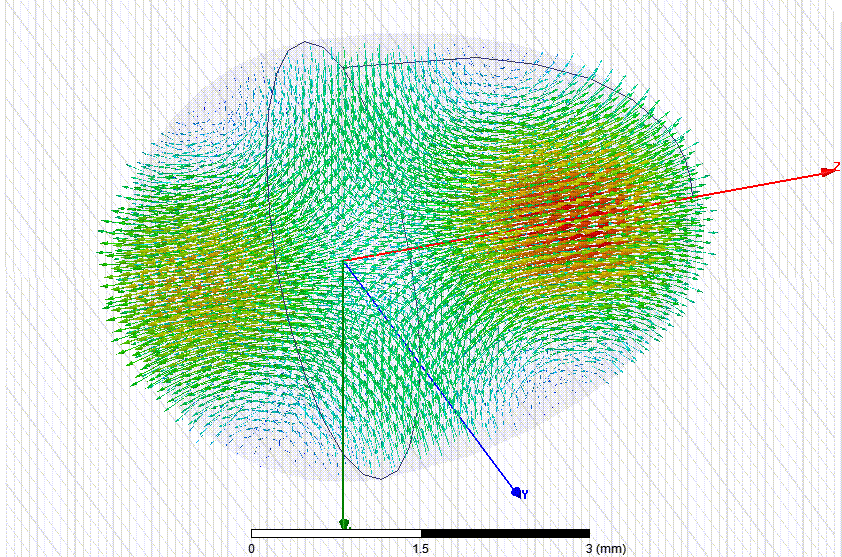
Измеряем параметры колебательных мод "шепчущей галереи" в рубиновых эллипсоидах разных размеров...
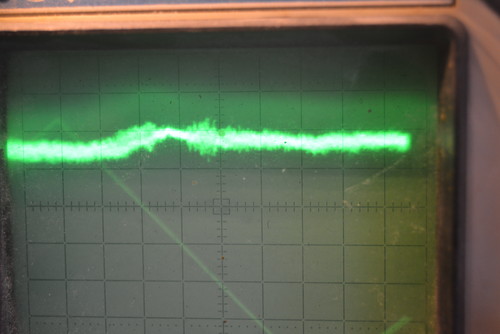









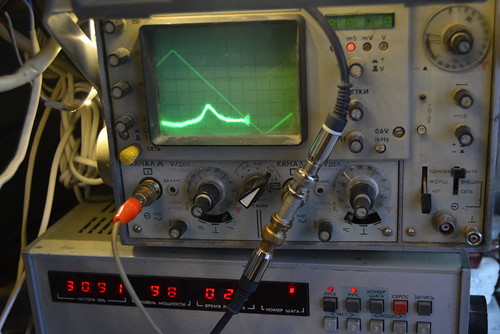


















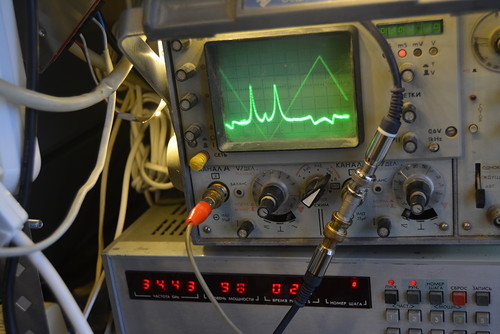




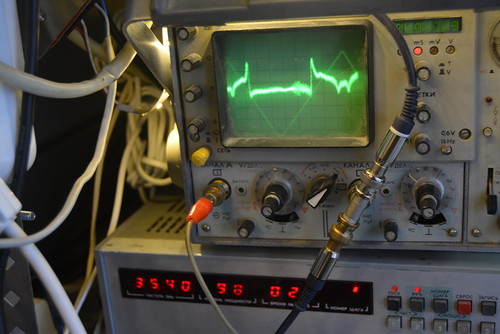



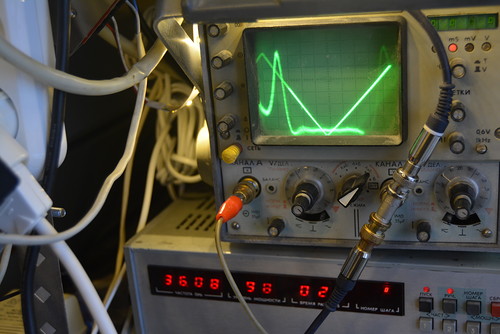
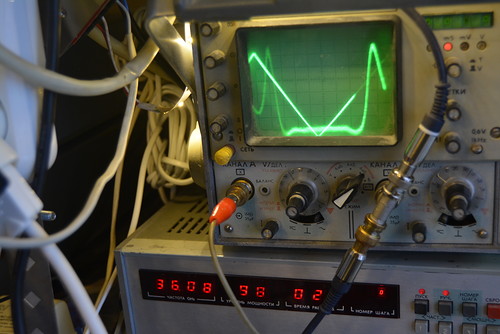
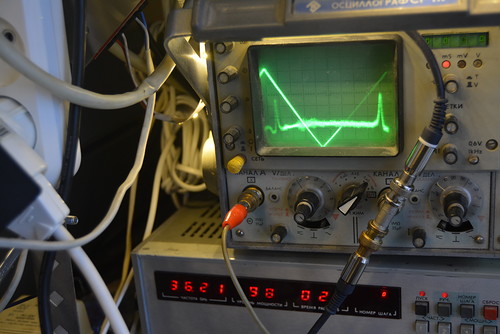


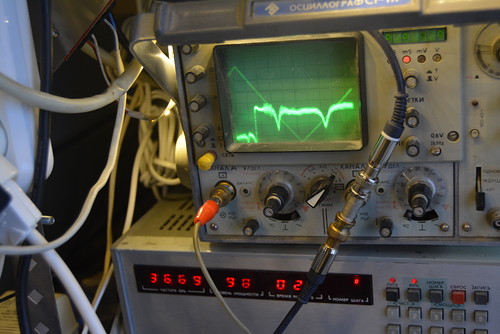





Переходим к резонатору длиной 20 мм и диаметром 12.18 мм. Это - не шлифованная заготовка из Китая.







Переходим к эллипсоидальному резонатору длиной 15 мм и диаметром 8.93 мм

Высокодобротных ( Q > 5000) резонансов обнаружить не удалось. Я начал рассматривать поверхность 15-мм эллипсоидов с большим увеличением и обнаружил случайные отклонения от идеальной фигуры вращения. Вероятно, подшипники станка, на котором изготавливались резонаторы длиной 15 мм были сильно изношены. Для низкочастотного объёмного резонанса это не имеет значения, а для мод шепчущей галереи имеет. Так что несколько заготовок придётся доработать на токарном станке для эксперимента в Дубне...
Фотографии "с Луны" не прошли геодезическую экспертизу...
Геодезисты обнаружили фальшивый фон, который использовали в НАСА для имитации лунных снимков:http://ligaspace.my1.ru/news/2011-06-23-314


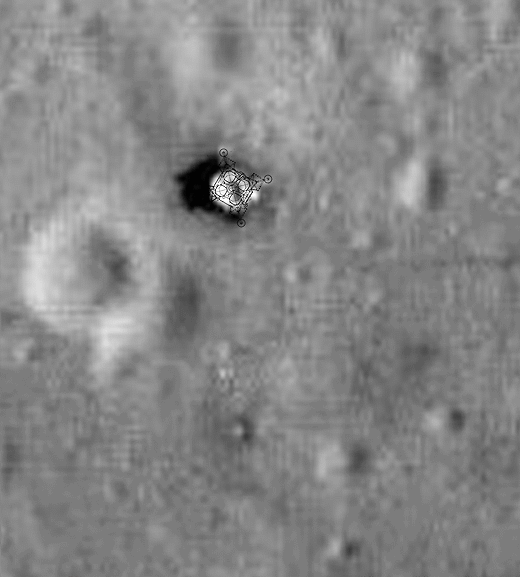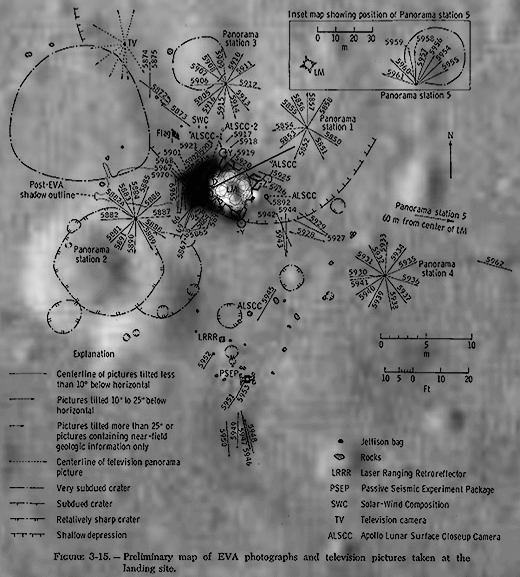
Расположение объектов на фотках "с Луны" не совпадает с фотографией лунной поверхности.
Уважаемые коллеги! Все, кто помогает создавать пикотехнологию, рубиновую энергетику, поднимает нашу цивилизацию на новую ступень развития. Всех нас можно поздравить с крупным успехом. Эксперименты в США, Германии и в Израиле подтвердили, что мы находимся на верном пути по трём главным научным направлениям лаборатории Наномир.
По теме "Рубиновая/микроволновая энергетика и транспорт" осталось сделать последний шаг, включить готовые источники энергии. Конечно, с помощью магнетрона миллиметрового диапазона создать рубиновую энергетику можно за считанные дни, но для этого нужно доделать номинальный ряд эллипсоидов и рубиновый энергетический конструктор.
Спасибо за поддержку!
Что нужно лаборатории для ближайших исследований:
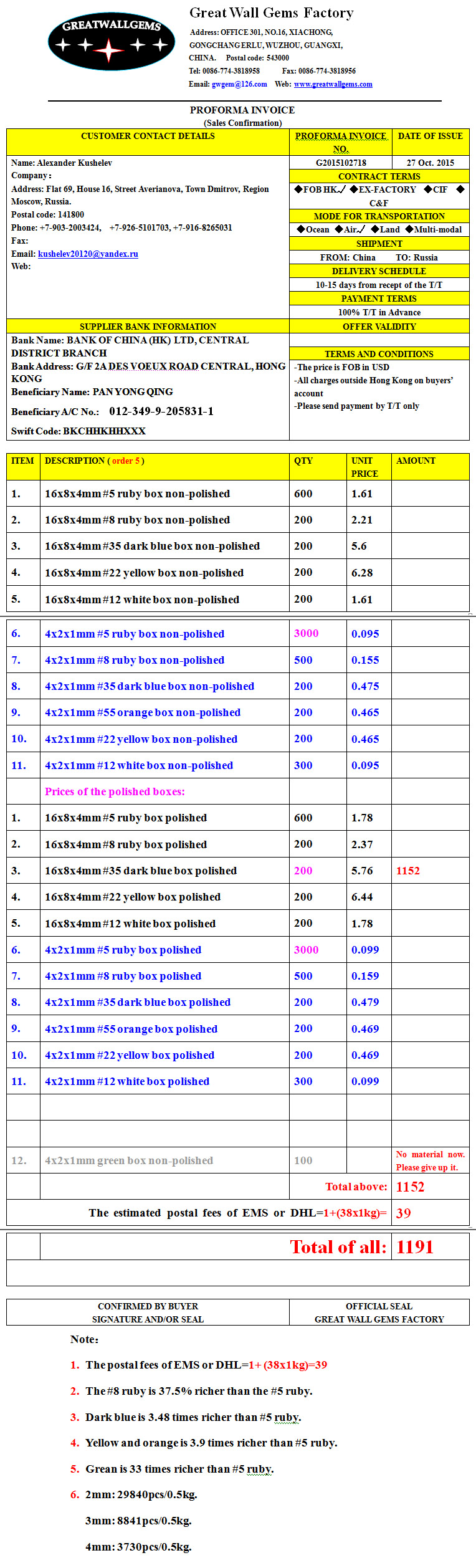
1. Заказать рубиновый и алмазный энергетические конструкторы. Минимальный комплект заказан. Следующая позиция стоит 1191 USD
2. Приобрести алмазные порошки и сверла для доработки эллипсоидов и "кирпичиков" (500 USD)
3. Оплатить покупку или аренду измерительной аппаратуры на диапазон от 4 до 32 ГГц. (От $1000). Идеальный вариант: http://www.keysight.com/en/pd-460865-pn-E8257D/psg-analog-signal-generator?&cc=RU&lc=rus
4. Начать третий этап создания средства для продления жизни: http://nanoworld.org.ru/topic/818/
5. Начать продажу книги "Пикотехнология белков":
Менеджеры, которые найдут заказы на структуры белков, получат 80% от суммы заказа!
Приглашение к сотрудничеству
|