
Выпуск 563
Лаборатория Наномир
Когда реальность открывает тайны,
уходят в тень и меркнут чудеса
...
Чётки Будды связывают градусы с игусами.

Чётки Будды состоят из 108 шариков.

Из 4 периодов/модулей получается система деления окружности на 108 будусов (216 полубудусов).
Лимб можно сделать из трех периодов по 36 цветных полос, т.е. 72 ряда бусин. В этом случае
из 3 периодов по 72 ряда бусин получается система, которая делит окружность
на 108 будусов (216 полубудусов)
из 4 периодов по 72 ряда бусин получается система, которая делит окружность на 288 игусов
из 5 периодов по 72 ряда бусин получается система, которая делит окружность на 360 градусов.
Таким образом из одного набора модулей можно собрать делительную систему Будды, Уилтширского "Наутилуса" и нашу, кстати, чью на самом деле?

Скрипт для 3DS Max:
-- Alien "108" tool. Alexander Kushelev. Nanoworld Lab.
a = #(); m = #(); re = #(100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,255,255,255,255,255,255,0,0,255,255,255,255,255,255)
g = #(100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,255,255,0,0,0,0,0,0,255,255,255,255,0,0)
b = #(255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0
,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0
,255,255,0,0,0,0,0,0,0,0,0,0,0,0)
for j = 1 to 11 do
(r = 1.75 - 0.125*cos (15*j)
a[j] = sphere radius: r position:[12 * cos(9.15* r * (j-1)), 12 * sin( 9.15 * r * (j-1)),0])
Select #(a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11])
Macros.run "Modifier stack" "Convert_to_mesh"
attach a[1] a[2]; attach a[3] a[4]; attach a[5] a[6]; attach a[7] a[8]; attach a[9] a[10]
attach a[1] a[11]; attach a[1] a[3]; attach a[1] a[5]; attach a[1] a[7]; attach a[1] a[9]
m[1] = copy a[1] wirecolor: [re[1],g[1],b[1]]; delete a[1]
move m[1] [-120,0,0]
for j = 1 to 54 do(re[j+54] = re[j]; g[j+54] = g[j]; b[j+54] = b[j])
for j = 1 to 108 do(re[j+108] = re[j]; g[j+108] = g[j]; b[j+108] = b[j])
for j = 1 to 216 do(m[j]=copy m[1] wirecolor: [re[j],g[j],b[j]]
m[j].pivot = [0,0,0]; alfa3=1.666666666666667*(j-1); rotate m[j]
alfa3 [0,1,0])

Скрипт для 3DS Max:
-- Alien "288" tools. Alexander Kushelev. Nanoworld Lab.
a = #(); m = #();
re = #(255,255,255,255,255,0,0,255,255,255,255,255)
g = #(0,0,255,255,255,0,0,0,0,0,255,255)
b = #(0,0,0,0,0,0,0,0,0,0,0,0)
for j = 13 to 48 do(re[j] = 0; g[j] = 100; b[j] = 255)
for j = 1 to 11 do (r = 1.75 - 0.125*cos (15*j)
a[j] = sphere radius: r position:[12 * cos(9.15* r * (j-1)), 12 * sin( 9.15 * r * (j-1)),0])
Select #(a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11])
Macros.run "Modifier stack" "Convert_to_mesh"
attach a[1] a[2]; attach a[3] a[4]; attach a[5] a[6]; attach a[7] a[8]; attach a[9] a[10]
attach a[1] a[11]; attach a[1] a[3]; attach a[1] a[5]; attach a[1] a[7]; attach a[1] a[9]
m[1] = copy
a[1] wirecolor: [re[1],g[1],b[1]]; delete a[1];move m[1] [-170,0,0]
for j = 1 to 48 do(re[j+48] = re[j]; re[j+96] = re[j]
g[j+48] = g[j]; g[j+96] = g[j]; b[j+48] = b[j]; b[j+96] = b[j])
for j = 1 to 144 do(re[j+144] = re[j]; g[j+144] = g[j]; b[j+144] = b[j])
for j = 1 to 288 do(m[j]=copy m[1] wirecolor: [re[j],g[j],b[j]]
m[j].pivot = [0,0,0]; alfa3=1.25*(j-1); rotate m[j] alfa3 [0,1,0])
-- Alien "108" tool. Alexander Kushelev. Nanoworld Lab.
a = #(); m = #(); re = #(100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,255,255,255,255,255,255,0,0,255,255,255,255,255,255)
g =
#(100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0,100,100,0,0
,255,255,0,0,0,0,0,0,255,255,255,255,0,0)
b = #(255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0
,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0,255,255,0,0
,255,255,0,0,0,0,0,0,0,0,0,0,0,0)
for j = 1 to 11 do
(r = 1.75 - 0.125*cos (15*j)
a[j] = sphere radius: r position:[12 * cos(9.15* r * (j-1)), 12 * sin( 9.15 * r * (j-1)),0])
Select #(a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11])
Macros.run "Modifier stack" "Convert_to_mesh"
attach a[1] a[2]; attach a[3] a[4]; attach a[5] a[6]; attach a[7] a[8]; attach a[9] a[10]
attach a[1] a[11]; attach a[1] a[3]; attach a[1]
a[5]; attach a[1] a[7]; attach a[1] a[9]
m[1] = copy a[1] wirecolor: [re[1],g[1],b[1]]; delete a[1]
move m[1] [-120,0,0]
for j = 1 to 54 do(re[j+54] = re[j]; g[j+54] = g[j]; b[j+54] = b[j])
for j = 1 to 108 do(re[j+108] = re[j]; g[j+108] = g[j]; b[j+108] =
b[j])
for j = 1 to 216 do(m[j]=copy m[1] wirecolor: [re[j],g[j],b[j]]
m[j].pivot = [0,0,0]; alfa3=1.666666666666667*(j-1); rotate m[j] alfa3 [0,1,0])

Скрипт для 3DS Max:
-- Fractal etalon. Nanoworld Lab. Alexander Kushelev
-- http://nanoworld.narod.ru
a = #(); m = #(); re = #(); g = #(); b = #()
for j = 1 to 11 do
(r = 1.75 - 0.125*cos (15*j)
a[j] = sphere radius: r position:[12 * cos(9.15* r * (j-1)), 12 * sin( 9.15 * r * (j-1)),0] wirecolor: [0,0,255])
Select #(a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11])
Macros.run "Modifier stack" "Convert_to_mesh"
attach a[1] a[2]; attach a[3] a[4]; attach a[5] a[6]; attach a[7] a[8];
attach a[9] a[10]
attach a[1] a[11]; attach a[1] a[3]; attach a[1] a[5]; attach a[1] a[7]; attach a[1] a[9]
m[1] = copy a[1] wirecolor: [0,0,255]; delete a[1]
move m[1] [-170,0,0]
for j = 1 to 37 do(
re[j] = 0; g[j] = 0; b[j] = 255)
re[38]=255; g[38]=255; b[38]=0
for j = 39 to 42 do(
re[j] = 255; g[j] = 0; b[j] = 0)
re[43]=0; g[43]=0; b[43]=0
for j = 44 to 47 do(
re[j] = 255; g[j] = 255; b[j] = 0)
re[48]=255; g[48]=0; b[48]=0
for j = 1 to 48 do(
re[j+48] = re[j]; re[j+96] = re[j]
g[j+48] = g[j]; g[j+96] = g[j]
b[j+48] = b[j]; b[j+96] = b[j])
for j = 1 to 144 do(
re[j+144] = re[j]; g[j+144] = g[j]; b[j+144] = b[j])
for j = 1 to 288 do(
m[j]=copy m[1] wirecolor: [re[j],g[j],b[j]]
m[j].pivot = [0,0,0]
alfa3=1.25*(j-1); rotate m[j] alfa3 [0,1,0])
Как работает инопланетный угломер?



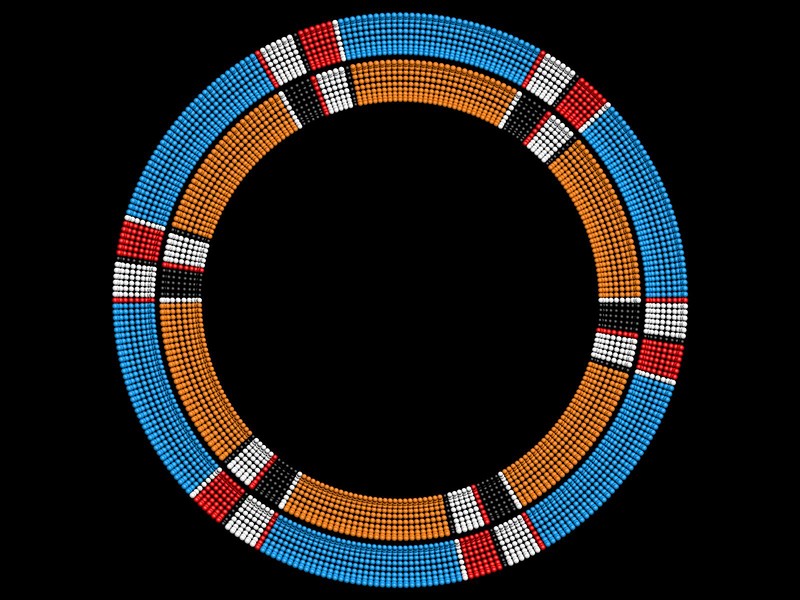
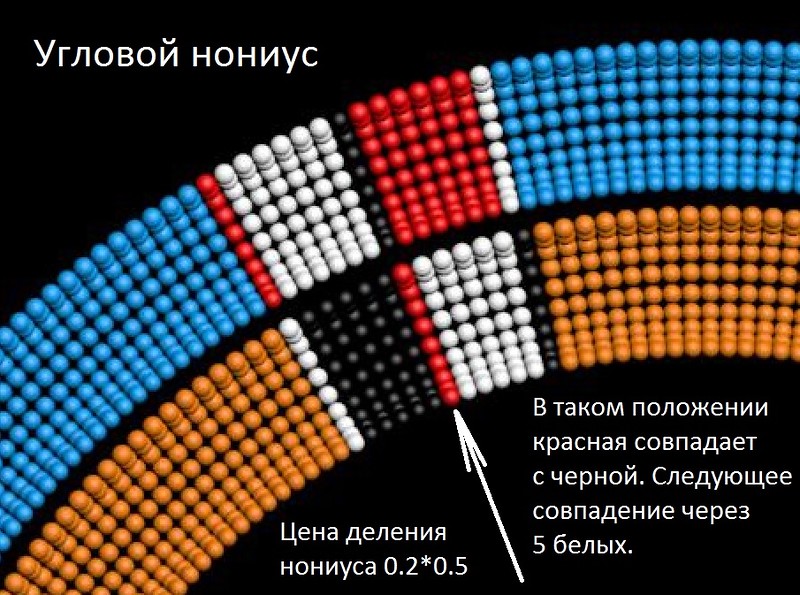
Вы обратили внимание на гирлянды флажков и углы между ними?


Цитата: Почему так стремятся залезть туда, даже современные мужчины и юноши? Неужели только ради приза? Вот и нет. Ими движет генетическая память. В древние времена залезть на столб обозначало пройти посвящение... Конец цитаты. Подробнее.
Цитата: Столб также ассоциируют с мировым деревом, связывающим три мира:
нижний – мир духов,
Кушелев: А для богов-инопланетян это всего лишь угломер...














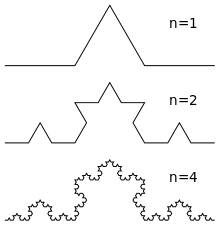




Нетрудно понять, что от пика звездолёта опускается не лестница (все инопланетяне могут летать на браслетах), а геодезическая рулетка.









Здесь опять хорошо видно, как встречные стрелки указывают на элемент рулетки.

Не так. В нижнем ряду мы видим 16 бусин под оранжевой полосой, а в верхнем ряду 5. Это значит, что переключение сигнала всех каналов будет происходить с дискретностью 32, т.е. на половинке маленькой бусинки. 32+24=56 единиц в периоде. Какие при этом будут сигналы в каналах "оранжевый", "красный", "голубой", "фиолетовый" и черно-белый, нужно разбираться.
Как же происходит измерения угла?
Рамка, которая отражена в этом изделии в виде бусины-бипирамиды, вращается перед бисерной структурой по кругу, т.е. вокруг головы. На самом деле для точных измерений нужно снять её с головы и правильно ориентировать на штативе. Совместить начало отсчёта с направлением на удаленный ориентир. Все удалённые наблюдатели, количество которых может быть любым, направляют активную оптическую систему ROBVW на угломер. При прохождении катафота через направление на наблюдателя, его оптическая система получает дополнительный световой импульс от бипирамидального катафота, который, кстати может быть совмещен с импульсным источником света. Этот импульс совмещается с периодическим сигналом от бусин. Далее логическая схема выдаёт угловую величину в системе "392". Точность измерения направления определяется погрешностью эталонной рулетки из шариков и катафота-бипирамиды.
Кстати, металлические кружочки на цепочках дают ещё один логический сигнал, дополняя систему функций Уолша...
Импульсный источник света, совмещённый с бипирамидальным катафотом может делить единицу угловой меры, например, на "минуты и секунды". При этом его сигнал тоже может кодироваться по дополнительным цветовым каналам, в частности, по каналу Yellow.


Понятно, что конструкция подвижной части угломера скопирована условно, но её можно восстановить. Представьте себе, что Вы увидели считывающее устройство лазерного диска:



Кстати, надевая эту бисерную структуру на цилиндры разных диаметров, можно переходить из системы градусов в систему игусов или в любую другую систему угловых мер...

Кстати, число оранжевых бусин в нижних двух рядах по 17, а в верхних - по 18. Скорее всего их везде должно быть по 16, т.е. отличие от 16 - издержки неправильных размеров бусин. И как уже отмечалось выше, элементарный угол определяется диаметром цилиндра, на котором одета бисерная структура. От бисерной структуры зависит лишь система сигналов Уолша, которая позволяет подсчитать количество элементарных сегментов, а их размер регулируется отдельно диаметром "головы".

Какой смысл возиться с долями градусов при построении 7-угольника, если под эту задачу можно иметь свою целочисленную шкалу?
Вероятно, набор из 6-7 шкал позволяет решить весь комплекс задач построения точных углов в целых числах. А электроника просто выбирает из всего набора функций Уолша наиболее подходящую для конкретной задачи. 6-7 специализированных угломеров решат типовую задачу быстрее и точнее одного универсального.
Такого типа угломер инопланетян тоже раздаёт направления в цифровом виде с точностью до тысячной доли угловой секунды.

Похоже, что фрактальный код с рулетки угломера считывается фрактальной рамкой, которая представляет собой оптическую систему, разрешения которой хватает, чтобы сформировать функции Уолша с точностью не хуже, чем это делает считывающая головка DVD.
Точность оцифровки угла определяется не только точностью фрактальной шкалы, но и точностью фрактальной рамки. Поэтому рамка тоже имеет многорядную структуру. Вероятно, реальная бисерная структура считывающей рамки представлена шестью рядами по 13 бусин в каждом. Точность считывания нижнего и верхнего кодов может быть небольшой. Важна точность считывания сигнала прохождения отдельных бусин. Для этого над ними проходит тоже 4 ряда по 13 бусин в каждом. Таким образом, считывани происходит параллельно по 13*4=52 каналам. После усреднения этот сигнал используется в качестве начала каждого "градуса". Между соседними градусами выдаётся сигнал начала угловых "минут" и сигнал начала угловых "секунд". Бипирамидальная бусина изображает направленный оптический излучатель, который направлен строго радиально. Наблюдатели получают направление в виде цифрового кода с точностью, которую обеспечивает эталонная бисерная структура. А эта точность в случае усреднения 52 сигналов соизмерима с точностью многорядной бисерной рулетки, т.е. достигать тысячных долей угловой секунды.






Здесь очевидно согласование структуры фрактальной рамки считывания со структурой фрактальной шкалы на разных расстояниях от центра угломера.

В частности, на считывающей головке самого маленького ожерелья-угломера красные и синие элементы расположены "крест-на-крест", диагонально, что характерно для мостовых схем сравнения. Подобные схемы в DVD еще не применяются...

Очевидно, что при одинаковом размере бусин, в рядах с бОльшим радиусом периоды содержат больше бусин. Это позволяет формировать функции Уолша с разным периодом в полярных координатах. В данной модели сектор, содержащий на внутренней дорожке по 5 синих/белых участков, по 4 бусины каждый (всего 20) на внешней дороже содержит 13 желтых и 13 черных бусин (всего 26). Таким образом, формируются функции Уолша с периодом 20 и 26 импульсов на сектор. А это значит, что на них можно построить периодическую функцию с периодом 13*10*2=260. Если числа будут 9 и 12, то можно получить 108 импульсов на сектор и т.д.

Мы видим RGB рамку считывания угла по паре жгутов с ортогональными цветными полосами и многоярусную систему нониусных шкал. 4 нониуса по радиусу от центра и 11 нониусов по радиусу к центру. Цифровой 15-разрядный нониус?
15 двоичных разрядов позволяют делить на 2^15=32768. Угловая секунда равна 1/3600 градуса и 1/1296000 части круга. 32768*360=11796480 Похоже, что угломеры инопланетян рассчитаны на точность 0.1 угловой секунды. Вероятно, температурные перекосы инструмента именно такого порядка, поэтому дальнейшее наращивание ярусов нониуса неэффективно. Системы шнуров безусловно круче, чем плоские диски, т.к. степень усреднения в них раза в три выше.
Посмотрим на разные типы головок / рамок угломеров...











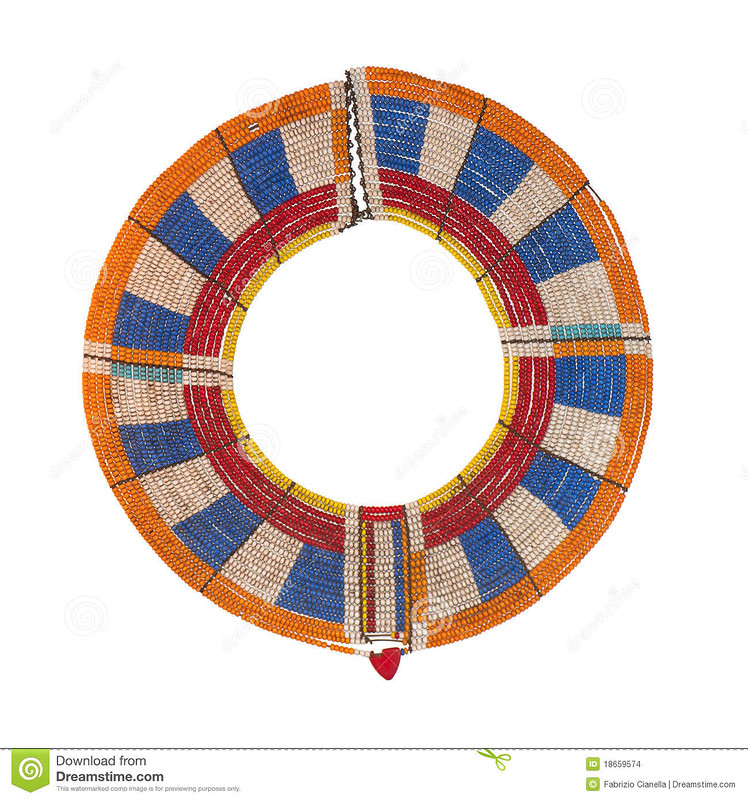


















Все догадались, как работают инопланетные угломеры? ![]()
Смоделируем этот угломер:

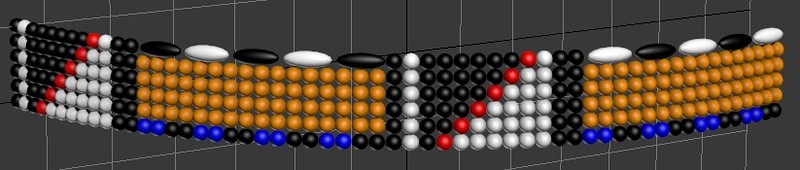
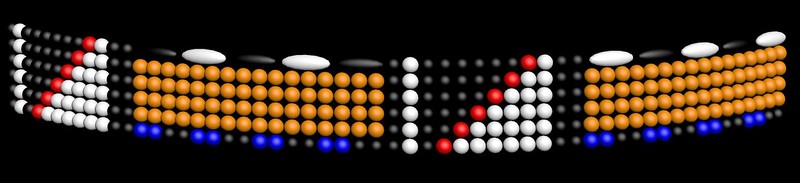
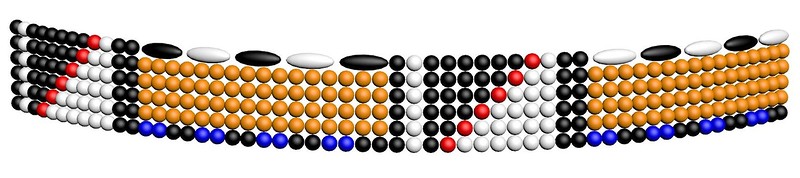
Скрипт для 3DS Max:
-- Alien tool . Alexander Kushelev. Nanoworld. Lab
-- http://nanoworld.narod.ru
a = #(); a2 = #(); a3 = #(); a4 =
#(); a5 = #(); a6 = #(); a7 = #(); m = #(); mm = #();
a_1 = #(); a2_1 = #(); a3_1 = #(); a4_1 = #(); a5_1 = #(); a6_1 = #(); a7_1 = #()
coltype = #([0,0,0],[255,255,255],[255,0,0],[0,255,0],[0,0,255],[255,255,0],[255,80,0])
-- 1-black, 2-white, 3-red, 4-green, 5-blue, 6-yellow,7-orange
col = #(1,2,1,3,2,2,2,2,2,2,1,1,5,5,1,1,5,5,1,1,5,5,1,1,5,5,1,1)
col2 = #(1,2,1,1,3,2,2,2,2,2,1,1,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7)
col3 = #(1,2,1,1,1,3,2,2,2,2,1,1,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7)
col4 = #(1,2,1,1,1,1,3,2,2,2,1,1,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7)
col5 = #(1,2,1,1,1,1,1,3,2,2,1,1,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7)
col6 = #(1,2,1,1,1,1,1,1,3,2,1,1,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7)
col7 = #(1,2,1,2,1)
col7_1 = #(2,1,2,1,2)
for j = 1 to 28 do
(a[j] = sphere radius: 1 position:[-64,0,0] wirecolor: coltype[col[j]]
a[j].pivot = [0,0,0]
a_1[j] = sphere radius: 1 position:[-64,0,0] wirecolor: coltype[col[j]]
a_1[j].pivot = [0,0,0]
a2[j] = sphere radius: 1
position:[-64,2,0] wirecolor: coltype[col2[j]]
a2[j].pivot = [0,0,0]
a2_1[j] = sphere radius: 1 position:[-64,2,0] wirecolor: coltype[col2[j]]
a2_1[j].pivot = [0,0,0]
a3[j] = sphere radius: 1 position:[-64,4,0] wirecolor: coltype[col3[j]]
a3[j].pivot = [0,0,0]
a3_1[j] = sphere radius: 1 position:[-64,4,0] wirecolor: coltype[col3[j]]
a3_1[j].pivot = [0,0,0]
a4[j] = sphere radius: 1 position:[-64,6,0] wirecolor: coltype[col4[j]]
a4[j].pivot = [0,0,0]
a4_1[j] = sphere radius: 1 position:[-64,6,0] wirecolor: coltype[col4[j]]
a4_1[j].pivot = [0,0,0]
a5[j] = sphere radius: 1 position:[-64,8,0] wirecolor: coltype[col5[j]]
a5[j].pivot = [0,0,0]
a5_1[j] = sphere radius: 1 position:[-64,8,0] wirecolor: coltype[col5[j]]
a5_1[j].pivot = [0,0,0]
alfa3=1.836734693877551*(j-1)
alfa3_28=alfa3+1.836734693877551*28
rotate a[j] alfa3 [0,1,0]
rotate a_1[j] alfa3_28 [0,1,0]
rotate a2[j] alfa3 [0,1,0]
rotate a2_1[j] alfa3_28 [0,1,0]
rotate a3[j] alfa3 [0,1,0]
rotate
a3_1[j] alfa3_28 [0,1,0]
rotate a4[j] alfa3 [0,1,0]
rotate a4_1[j] alfa3_28 [0,1,0]
rotate a5[j] alfa3 [0,1,0]
rotate a5_1[j] alfa3_28 [0,1,0])
for j = 1 to 12 do
(a6[j] = sphere radius: 1 position:[-64,10,0] wirecolor: coltype[col6[j]]
a6[j].pivot = [0,0,0]
a6_1[j] = sphere radius: 1 position:[-64,10,0] wirecolor: coltype[col6[j]]
a6_1[j].pivot = [0,0,0]
alfa3=1.836734693877551*(j-1)
alfa3_28=alfa3+1.836734693877551*28
rotate a6[j] alfa3 [0,1,0]
rotate a6_1[j] alfa3_28 [0,1,0])
alfa0 = 1.836734693877551*(12+2.5/2)
for j = 1 to 5 do
(a7[j] = sphere radius: 1 position:[-64,10,0] wirecolor: coltype[col7[j]]
scale a7[j] [1,1,16/5]
a7[j].pivot = [0,0,0]
a7_1[j] = sphere radius: 1 position:[-64,10,0] wirecolor:
coltype[col7_1[j]]
scale a7_1[j] [1,1,16/5]
a7_1[j].pivot = [0,0,0]
alfa4=alfa0 + (1.836734693877551*(j-1)*16/5)
alfa4_28=alfa4+1.836734693877551*28
rotate a7[j] alfa4 [0,1,0]
rotate a7_1[j] alfa4_28 [0,1,0])
Конечно, интерес к подобным угломерам меркнет на фоне считывающих дисков:

Поэтому начнём моделировать их...
Фрактальная обработка информации. Считывающие ... диски!
От считывающих головок к считывающим ... дискам!

Кстати, похоже, что инопланетяне используют наряду с бесцветным цветное оптоволокно, что может снижать уровни шумов...
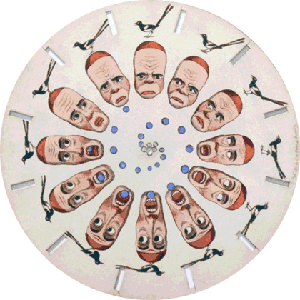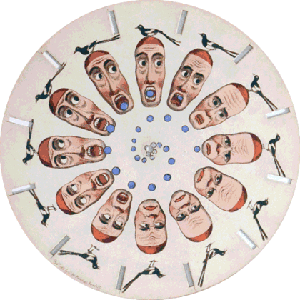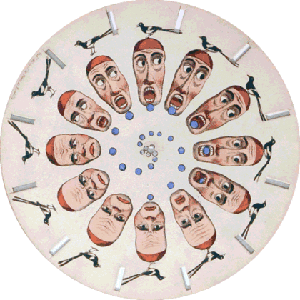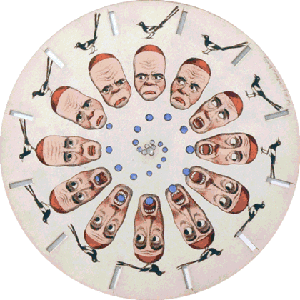
Подобные диски могут работать в разных режимах.
1. Режим передачи максимального объёма информации. В этом случае информация не дублируется, но объём её максимален.
2. Режим передачи информации с максимальной точностью / надёжностью. В этом случае информация многократно дублируется / усредняется.
Представьте себе, что Вы увидите, если наложить полупрозрачный орнамент такого типа:

На непрозрачный орнамент, который является зеркальным отражением этого:

Получится один из орнаментов с африканских копий угломеров! А теперь будем медленно двигать полупрозрачный орнамент вдоль непрозрачного. Получится "калейдоскоп" с плавно изменяющимися узорами, которые фактически такие же, как на этом голубом диске:

Величина угла поворота кодируется цветовым спектром! Мы знаем, что спектральные методы очень точные, поэтому с помощью спектра можно передать точное значение угла поворота.

Maasai Necklace


Скрипт для 3DS Max, который строит модель считываемого диска:
-- Alien tool . Alexander Kushelev. Nanoworld. Lab
-- http://nanoworld.narod.ru
a = #(); a1 = #(); a2 = #(); a3 = #(); a4 = #(); a5 = #(); a6 = #(); a7 = #(); a8 = #(); a9 = #()
a10 = #(); a11 = #(); a12 = #(); a13 = #(); a14 = #(); a15 = #(); a16 = #(); a17 = #(); a18 = #()
a19 = #(); a20 = #(); a21 = #(); a22 = #(); a23 = #(); a24 = #(); a25 = #(); a26 = #(); a27 = #()
a28 = #(); a29 = #(); a30 = #(); a31 = #(); a32 = #(); a33 = #(); a34 = #(); a35 = #(); a36 = #(); a37 = #()
alfa=1.836734693877551
for j = 6 to 30 do
(a[j] = sphere radius: 1 position:[-64,0,0] wirecolor: [0,0,255]; a[j].pivot = [0,0,0]
a1[j] = sphere radius: 1 position:[-64,2,0] wirecolor: [0,0,255]; a1[j].pivot = [0,0,0]
a2[j] = sphere radius: 1 position:[-64,4,0] wirecolor: [0,0,255]; a2[j].pivot = [0,0,0]
a3[j]
= sphere radius: 1 position:[-64,6,0] wirecolor: [0,0,255]; a3[j].pivot = [0,0,0]
a4[j] = sphere radius: 1 position:[-64,8,0] wirecolor: [0,0,255]; a4[j].pivot = [0,0,0]
a5[j] = sphere radius: 1 position:[-64,10,0] wirecolor: [0,0,255]; a5[j].pivot = [0,0,0]
a6[j] = sphere radius: 1 position:[-64,12,0]
wirecolor: [0,0,255]; a6[j].pivot = [0,0,0]
a7[j] = sphere radius: 1 position:[-64,14,0] wirecolor: [0,0,255]; a7[j].pivot = [0,0,0]
a8[j] = sphere radius: 1 position:[-64,16,0] wirecolor: [0,0,255]; a8[j].pivot = [0,0,0]
a9[j] = sphere radius: 1 position:[-64,18,0] wirecolor: [0,0,255]; a9[j].pivot
= [0,0,0]
a10[j] = sphere radius: 1 position:[-64,20,0] wirecolor: [0,0,255]; a10[j].pivot = [0,0,0]
a11[j] = sphere radius: 1 position:[-64,22,0] wirecolor: [0,0,255]; a11[j].pivot = [0,0,0]
a12[j] = sphere radius: 1 position:[-64,24,0] wirecolor: [0,0,255]; a12[j].pivot = [0,0,0]
a13[j] = sphere radius: 1 position:[-64,26,0] wirecolor: [0,0,255]; a13[j].pivot = [0,0,0]
a14[j] = sphere radius: 1 position:[-64,28,0] wirecolor: [0,0,255]; a14[j].pivot = [0,0,0]
a15[j] = sphere radius: 1 position:[-64,30,0] wirecolor: [0,0,255]; a15[j].pivot = [0,0,0]
a16[j] = sphere radius: 1 position:[-64,32,0] wirecolor: [0,0,255]; a16[j].pivot = [0,0,0]
a17[j] = sphere radius: 1 position:[-64,34,0] wirecolor: [0,0,255]; a17[j].pivot = [0,0,0]
a18[j] = sphere radius: 1 position:[-64,36,0] wirecolor: [0,0,255]; a18[j].pivot = [0,0,0]
a19[j] = sphere
radius: 1 position:[-64,36,0] wirecolor: [0,0,255]; a19[j].pivot = [0,0,0]
a20[j] = sphere radius: 1 position:[-64,34,0] wirecolor: [0,0,255]; a20[j].pivot = [0,0,0]
a21[j] = sphere radius: 1 position:[-64,32,0] wirecolor: [0,0,255]; a21[j].pivot = [0,0,0]
a22[j] = sphere radius: 1 position:[-64,30,0]
wirecolor: [0,0,255]; a22[j].pivot = [0,0,0]
a23[j] = sphere radius: 1 position:[-64,28,0] wirecolor: [0,0,255]; a23[j].pivot = [0,0,0]
a24[j] = sphere radius: 1 position:[-64,26,0] wirecolor: [0,0,255]; a24[j].pivot = [0,0,0]
a25[j] = sphere radius: 1 position:[-64,24,0] wirecolor:
[0,0,255]; a25[j].pivot = [0,0,0]
a26[j] = sphere radius: 1 position:[-64,22,0] wirecolor: [0,0,255]; a26[j].pivot = [0,0,0]
a27[j] = sphere radius: 1 position:[-64,20,0] wirecolor: [0,0,255]; a27[j].pivot = [0,0,0]
a28[j] = sphere radius: 1 position:[-64,18,0] wirecolor: [0,0,255]; a28[j].pivot =
[0,0,0]
a29[j] = sphere radius: 1 position:[-64,16,0] wirecolor: [0,0,255]; a29[j].pivot = [0,0,0]
a30[j] = sphere radius: 1 position:[-64,14,0] wirecolor: [0,0,255]; a30[j].pivot = [0,0,0]
a31[j] = sphere radius: 1 position:[-64,12,0] wirecolor: [0,0,255]; a31[j].pivot = [0,0,0]
a32[j] = sphere radius: 1 position:[-64,10,0] wirecolor: [0,0,255]; a32[j].pivot = [0,0,0]
a33[j] = sphere radius: 1 position:[-64,8,0] wirecolor: [0,0,255]; a33[j].pivot = [0,0,0]
a34[j] = sphere radius: 1 position:[-64,6,0] wirecolor: [0,0,255]; a34[j].pivot = [0,0,0]
a35[j] = sphere radius: 1 position:[-64,4,0] wirecolor: [0,0,255]; a35[j].pivot = [0,0,0]
a36[j] = sphere radius: 1 position:[-64,2,0] wirecolor: [0,0,255]; a36[j].pivot = [0,0,0]
a37[j] = sphere radius: 1 position:[-64,0,0] wirecolor: [0,0,255]; a37[j].pivot = [0,0,0]
alfa1=alfa*(j-1); alfa2=alfa*j; alfa3=alfa*(j+1); alfa4=alfa*(j+2)
alfa5=alfa*(j+3); alfa6=alfa*(j+4); alfa7=alfa*(j+5)
rotate a[j] alfa1 [0,1,0]; rotate a1[j] alfa2 [0,1,0]; rotate a2[j] alfa3 [0,1,0]
rotate a3[j]
alfa4 [0,1,0]; rotate a4[j] alfa5 [0,1,0]; rotate a5[j] alfa6 [0,1,0]
rotate a6[j] alfa7 [0,1,0]; rotate a7[j] alfa6 [0,1,0]; rotate a8[j] alfa5 [0,1,0]
rotate a9[j] alfa4 [0,1,0]; rotate a10[j] alfa3 [0,1,0]; rotate a11[j] alfa2
[0,1,0]
rotate a12[j] alfa1 [0,1,0]; rotate a13[j] alfa2 [0,1,0]; rotate a14[j] alfa3 [0,1,0]
rotate a15[j] alfa4 [0,1,0]; rotate a16[j] alfa5 [0,1,0]; rotate a17[j] alfa6 [0,1,0]
rotate a18[j] alfa7
[0,1,0]; rotate a19[j] -alfa7 [0,1,0]; rotate a20[j] -alfa6 [0,1,0]
rotate a21[j] -alfa5 [0,1,0]; rotate a22[j] -alfa4 [0,1,0]; rotate a23[j] -alfa3 [0,1,0]
rotate a24[j] -alfa2 [0,1,0]; rotate a25[j] -alfa1 [0,1,0]; rotate a26[j] -alfa2 [0,1,0]
rotate a27[j] -alfa3 [0,1,0]; rotate a28[j] -alfa4 [0,1,0]; rotate a29[j] -alfa5 [0,1,0]
rotate a30[j] -alfa6 [0,1,0]; rotate a31[j] -alfa7 [0,1,0]; rotate a32[j] -alfa6 [0,1,0]
rotate a33[j] -alfa5 [0,1,0]; rotate a34[j]
-alfa4 [0,1,0]; rotate a35[j] -alfa3 [0,1,0]
rotate a36[j] -alfa2 [0,1,0]; rotate a37[j] -alfa1 [0,1,0])
Скрипт для модели считывающего диска отличается радиусами шариков. Вместо 1 все радиусы равны 0.7
Выводим формулу погрешности фрактального эталона
Материал с форума лаборатории Наномир:
aest: Я участвую, внося существенные замечания.
Кушелев: Одна формула была бы полезнее массы слов ![]()
Кстати, я эту формулу могу и сам написать.
Формула усреднения погрешностей фрактальных эталонов Кушелева:
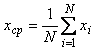
Но 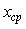 будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем отдельные шарики.
будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем отдельные шарики.
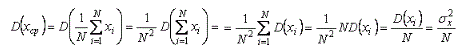
Откуда 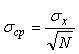
Поскольку 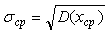
Однако эксперимент показывает, что погрешность фрактального эталона длины с ростом числа рядов элементов уменьшается быстрее, чем по этой формуле. Это связано с дополнительным механизмом уменьшения погрешности. Он работает следующим образом. Если размер элемента существенно меньше среднего, то образуются зазоры между этим элементом и соседними элементами, расположенными вдоль. Если же размер элемента существенно больше среднего, то он выталкивается за пределы плоскости эталона и тоже не влияет на длину эталона.





Уважаемые коллеги! Все, кто помогает создавать пикотехнологию, рубиновую энергетику, поднимает нашу цивилизацию на новую ступень развития. Всех нас можно поздравить с крупным успехом.Эксперименты в США, Германии и в Израиле подтвердили, что мы находимся на верном пути по трём главным научным направлениям лаборатории Наномир.
По теме "Рубиновая/микроволновая энергетика и транспорт" осталось сделать последний шаг, включить готовые источники энергии. Конечно, с помощью магнетрона миллиметрового диапазона создать рубиновую энергетику можно за считанные дни, но для этого нужно доделать номинальный ряд эллипсоидов и рубиновый энергетический конструктор.
Спасибо за поддержку!


Что нужно лаборатории для ближайших исследований:
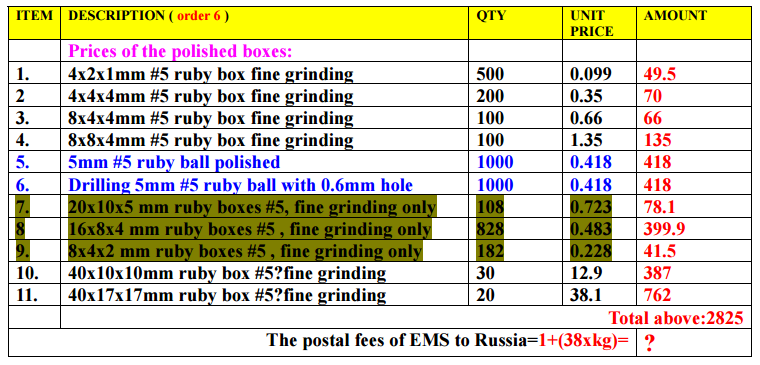
Из крупных рубиновых блоков (40x17x17mm) будут иготовлены составные рубиновые резонаторы для включения в микроволновой печи:

Skype, 2016-04-25:
[12:51:45] Jocie Lee: Now we have round shape . the maximum size is 11mm


[13:26:01] Jocie Lee: The price is 773 usd/pcs
[13:30:11] Кушелев Александр Юрьевич: Thank You very mach!
[13:31:24] Кушелев Александр Юрьевич: Do You have diamond box (color, for example yellow) 4x4x1mm ? If Yes, need price...

[13:33:50] Кушелев Александр Юрьевич: And I need this forms:

[13:59:46] Jocie Lee: oh...I am sorry. We dont sell box
[14:02:33] Кушелев Александр Юрьевич: OK! I wait money from my investors. I need 773usd/pcs diamond.
[14:02:49] Jocie Lee: OK
[14:03:13] Кушелев Александр Юрьевич: Do You make color diamonds?

[14:04:50] Jocie Lee: I think this colorful stone is cubic zirconia
[14:05:23] Кушелев Александр Юрьевич: But I need color synthetic diamonds for science experiments :)
[14:06:50] Кушелев Александр Юрьевич: I have cubic zirconia, but it has bad electromagnetic parameters. I need color synthetic diamond only. Your diamond size is very good!
1. Заказать рубиновый и алмазный энергетические конструкторы.
Минимальный комплект заказан. Следующая позиция стоит 1191 USD
2. Приобрести алмазные порошки и сверла для доработки эллипсоидов и "кирпичиков" (500 USD)
3. Оплатить покупку или аренду измерительной аппаратуры на диапазон от 4 до 32 ГГц. (От $1000). Идеальный вариант: http://www.keysight.com/en/pd-460865-pn-E8257D/psg-analog-signal-generator?&cc=RU&lc=rus
4. Начать третий этап создания средства для продления жизни: http://nanoworld.org.ru/topic/818/
5. Начать продажу книги "Пикотехнология белков":
Менеджеры, которые найдут заказы на структуры белков, получат 80% от суммы заказа!
Приглашение к сотрудничеству
|