Перевод осуществил Pavel A. Chuvanov, участник проекта Almighty.

Кинематика — есть процесс вычисление позиции в пространстве для конца взаимосвязанной структуры при заданных углах поворота всех шарнирных точек (Joints). Это легко осуществляется, если есть только одно решение. Инверсная кинематика делает обратное. Для данной конечной точки вычисляются необходимые углы поворота шарниров таким образом, чтобы удалось достичь этой конечной точки. При этом могут возникнуть трудности, если есть много или бесконечно много решений.

Данный процесс чрезвычайно полезен в робототехнике. Например, вы захотели, чтобы рука робота потянулась и взяла объект. Если программа знает местоположение объекта относительно плечевого сустава, то ей достаточно расчитать углы поворота шарниров чтобы достичь объекта. Также инверсная кинематика полезна в 3D играх. Возьмем для примера дракона с очень длинной шеей. Дракон должен реалистично изогнуть шею и слопать игрока стоящего на полу. Или игрок захотел поднять с пола некий объект или нажать на кнопку. Пользователь увидит на экране как игрок потянется и коснется объекта, вместо того чтобы просто махнуть рукой где-то вблизи объекта (как например в Alone In The Dark).

Я написал небольшую демку под DOS иллюстрирующую механизм инверсной кинематики. Скриншот показывает как змейка пытается коснуться небольшого вращающегося кубика. Вы можете перемещать цель используя клавиатуру. В демке на змейку действует гравитация и она обладает небольшой эластичностью, поэтому возможно будет двигаться и после того как найдет цель, пытаясь достичь более комфортного положения. Модель змейки находится в файле tail.cfg. Вы можете исправить его чтобы создать какой-нибудь другой объект.

Нет решений

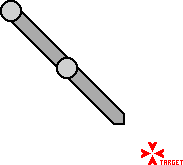
Существует много случаев, когда связанная структура не в состоянии достичь цели. Например вы не можете коснуться локтем одной руки запястья той же руки. Или достать с земли до верхушки высокого дерева.

Одно решение

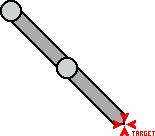
Два решения

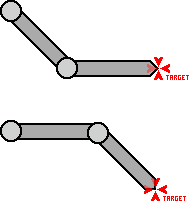
В случае если есть два решения, то должна существовать техника выбора, какое из решений больше отвечает текущему состоянию структуры.

Много решений

Когда используется более двух шарниров, часто случается, что существует много решений задачи. Тем не менее, некоторые решения являются лучше других. Если ваша структура представляет, например, руку то некоторые решения более удобны, другие очень неестественны. Часто есть оптимальное решение.

Об алгоритме

Я пришел к методу инверсной кинематики после некоторых раздумий, проб и ошибок. Нет сомнений, что есть много алгоритмов решения проблем инверсной кинематики, но здесь я опишу только один.

Этот алгоритм не сразу находит решение. Это не простая функция где вы задаете место назначения и получаете углы. Это итеративный алгоритм, что делает алгоритм более реалистичным в программах, особенно в играх, где вы наверяка хотите, чтобы объекты двигались сглажено.

Решение находится за счет виртуального применения силы к концу цепочки и перетаскивания конца цепочки в конечную позицию. Сила действует на каждое сочленение и двигает структуру немного ближе к конечной точке. Так что даже если решения нет, цепочка приблизится к конечной точки так близко, насколько это возможно. Так как шарниры рассчитываются раздельно, то вы можете задать им разные свойства, такие как жесткость, эластичность и т.д. Каждый из шарниров также может иметь оптимальную позицию, которую алгоритм будет пытаться достичь так близко, как только это возможно.

Инверсная кинематика в 2D

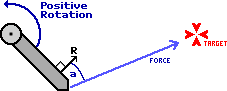
Начнем с одного шарнира. В данном случае он может вращаться вокруг только одной оси (направление против часовой стрелки выберем как положительное). Вектор R действует под прямым углом к кости. Вектор силы F действует от конечной точки в направлении цели. Угол между R и F есть a. Теперь все совсем просто. Скорость, с которой вы должны поворачивать шарнир, пропорциональна скалярному произведению (dot product) векторов R и F. Придерживаясь точки зрения, что скалярное произведение двух векторов положительное число, и, конечно же, шарнир должен вращаться в положительном направлении, чтобы максимально приблизится к цели. Если угол между R и F прямой, то шарнир повернулся так, чтобы кость была максимально близко к цели и поэтому шарнир не должен больше поворачиваться. В этой точке скалярное произведение двух векторов даст ноль.

torque = (RF) * k

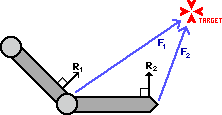
Ну вот, приехали. Случай потяжелее. Впредь, все будет просто разновидностью данного случая. Когда вы имеете больше одной кости вы просто должны повторить вышеописанный алгоритм для каждого шарнира по очереди.

Начнем с шарнира ближайшего к цели:
1. Вычислим вектор силы (от конечной точки к цели)
2. Вычислим скалярное произведение вектора силы и вектора, перпендикулярного кости.
3. Умножим скалярное произведение на небольшое число (например 0.01)
4. Добавим его к углу шарнира.

Делаем так для всех шарниров последовательно.

Инверсная кинематика в 3D

В трехмерном пространстве вычисления будут не намного сложнее. Есть три возможных оси, вокруг которых шарнир может вращаться. Я попытался применить вышеописанный метод в трехмерном пространстве, но результаты были не слишком хорошими. Я не до конца понял почему. Тем не менее эта математика безусловно работает. Есть нечто, что требует большого количества изменений установок, чтобы все работало, безусловно, правильно.

Ну, что ж, двигаемся дальше.

Ось шарнира перпендикулярна кости

Сперва давайте попробуем пример, приведенный выше, но в этот раз в 3D. Это система с двумя шарнирами и мы сперва возьмем первый шарнир.

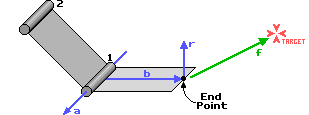
Дадим названия векторам
a - Вектор вдоль оси шарнира.
b - Вектор вдоль кости.
r - Вектор перпендикулярный a и b.
f - Вектор силы (действующий от конечной точки к цели).

Если вектор силы будет параллелен a, шарнир не будет вращаться. Если он параллелен b, то вы просто тащите кость, шарнир не будет вращаться. Вооружившись данными пустулатами, я решил что вращающий момент должен быть пропорционален синусу угла между a и f и синусу угла между b и f.

Если конечная точка пришла в точку цели, то вы не хотите, чтобы структура двигалась, но если конечная точка далеко от цели, то вы хотите, чтобы структура двигалась быстро. Следовательно, вращающий момент должен быть пропорционален длине вектора силы.

Есть только одна вещь, которую нельзя понять из вышеописанного - направление в котором должен вращаться шарнир. Пусть шарнир должен вращатсья в положительном направлении если вектор силы направлен вдоль r, и в противоположном направлении в случае если вектор силы направлен противоположно r.

Сложив все воедино получим:

torque = Mag(f) * SinVect(a, f) * SinVect(b, f) * sign(CosVect(r, f)) * Sensitivity

В данной формуле SinVect и CosVect возвращают соответственно синус и косинус угла между векторами. Mag возвращает длину вектора, и sign возвращает знак числа. Sensitivity - это просто небольшая скалярная константа.

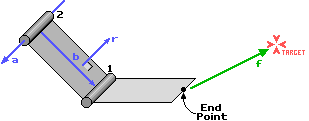
Теперь вы можете двигаться к следующему шарниру в структуре. Вычислим новые значения векторов a,b и f, и вычислим крутящий момент для шарнира 2. Вычислим крутящий момент для всех шарниров в структуре и добавим к углу каждого шарнира по его крутящему моменту. Конечная точка должна теперь быть ближе к цели. Непрерывно повторяя процесс мы сможем приблизить конечную точку структуры к цели максимально близко или даже коснутся цели.

Ось шарнира направлена вдоль кости

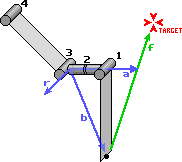
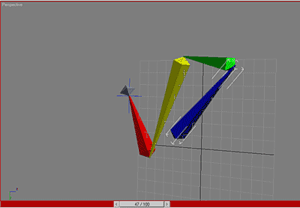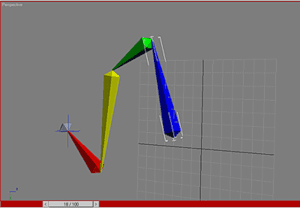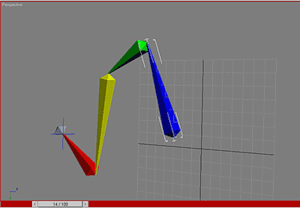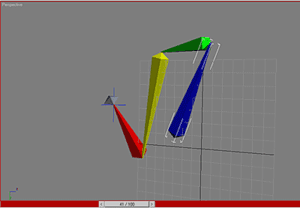
Хорошо, давайте взглянем на более трудный случай. Но здесь нет ничего нового. Здесь вы видите связанную структуру состоящую из четырех шарниров. Шарнир номер два, тем не менее, может вращаться вокруг оси своей кости. Это похоже на изгиб вашего запястья. И конечно этот шарнир наиболее важен. Как и в предыдущем случае, вектор a будет проходить вдоль оси шарнира, но в этом случае это еще и вдоль кости. Вектор b сейчас идет от шарнира к конечной точке. Вектор r как и раньше перпендикулярен обоим.

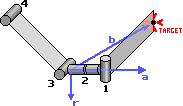
Чтобы достичь цели шарнир 2 должен повернуться на 90 градусов (см. правую картинку).

И закончим тем, что вектор b различен для шарниров чья ось вращения параллельна кости.

Дополнительные замечания.

Теперь, когда вы освоили базу инверсной кинематики, есть еще задача регулировки системы, чтобы задать ее поведение в различных ситуациях. Как я говорил до этого, есть много разных решений. Некоторые лучше, некоторые хуже. Различаются тем как они смотрятся, величиной затраченных движений или удобством.

Сглаживание кривых

Реальная змейка на реальной анимации редко когда запутывается сама в себе. Она имеет тенденцию образоввывать довольно гладкие кривые. Змейка в демке сделана из пар шарниров оси, которые перпендикулярны друг другу. Первоначально написанная змейка двигалась не слишком реалистично. Поэтому я добавил ей немного элластичности в шарнирах. Из-за этого шарниры сопротивляются изгибу. Чем больше вы их сгибаете, тем более они сопротивляются. Эффект от этого такой, что изгиб разпространяется по шарнирам.

Давайте взглянем на динозавра. Он очень толстый в теле, но становится более тонким и гибким в шее. Это свойство может быть симулировано связанной структурой, сочленения которой все более и более элластичны к концу.

Удобное положение

Конечности предпочитают находится в удобном положении. Это может быть выполнено новым добавлением элластичности шарнирам. Тем не менее в этом случае может быть наилучшим иметь определенный ряд положений для каждого шарнира в котором нету сопротивления. Этот ряд может быть рассмотен как удобный. После того как шарнир покидает удобное положение он будет сопротивлятся все сильнее и сильнее пока совсем не откажется вращаться.

Также может быть желательно держать конечность максимально низко. Люди редко долго держат свои руки на весу более, чем это необходимо. Поэтому положение выбирается исходя из минимальной энергии требующейся для удерживания положения.

Оригинал: http://freespace.virgin.net/hugo.elias/models/m_ik.htm

8 июня 2002