Выпуск 219

 Лаборатория Наномир

Когда реальность открывает тайны,
уходят в тень и меркнут чудеса ...

Прямая трансляция Ярослава Старухина из лаборатории Наномир.

2011/02/06 cостоялась интернет-трансляция Ярослава Старухина из лаборатории Наномир.

Я рассказал о создании пикотехнологии

Показывая материал на экране компьютера, я давал номера выпусков рассылки "Новости лаборатории Наномир"

Интернет-телезрители могли открыть соответствующий выпуск рассылки и ознакомиться с материалом в оригинальном качестве и в удобном для них темпе.

  

Те, кто не успел задать свои вопросы или получить на них ответы во время интернет-трансляции, могут продолжить научную дискуссию на форуме лаборатории Наномир. Интернет-трансляция длилась более трёх часов. На видеокамеру записано более 13 Gb. Желающие могут заказать копию этой трансляции на 3DVD, а то, что не уместилось, можно посмотреть на сервере или заказать на дополнительном диске.

Фрагмент 1. Люба демонстрирует резонаторы, предназначенные для эксперимента в Дубне.

Фрагмент 2. Завершающее слово Ярослава Старухина.

Анатолий Шестопалов записал интернет-трансляцию и выложил на своём блоге.

Обсуждение на форуме лаборатории Наномир.

Взвешенные, разностные и др. фракталы Кушелева.

 

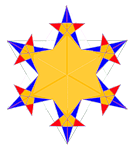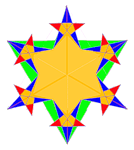
Материал с форума лаборатории Наномир:

Trilobit: Установлено, что кондитеры и хлебопёки из поколения в поколение передают потомкам формы источников энергии и двигателей.

Кушелев: Вы правы.

При этом нужно отметить, что кондитеры не могли изобрести "кривой орнамент", т.е. они пытались копировать более симметричный оригинал. Согласны?

Симметрия позволяет реконструировать оригинал даже в случае частичного повреждения копии.

В форме некоторых кондитерских изделий угадывается инопланетная техника.

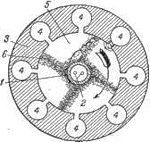
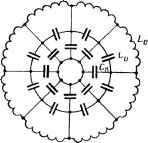
Вот её земные аналоги. Кстати, почти готовый орнамент для печенья

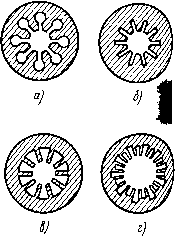
Вы покажите кондитерам эту картинку и спросите, могут ли они изготовить печенье с таким орнаментом?

А ещё спросите кондитеров, которые делают такие печенья, знают ли они, что форма этого печенья повторяет форму фрактала на основе кривой Коха?

По современной классификации форма печенья, показанного выше, соответствует префракталу второго порядка. Хотя ... это другой тип фрактала. Сейчас мы его смоделируем...

 

 Взвешенный фрактал Кушелева (префракталы 0,1,2-го порядков)

Взвешенный фрактал Кушелева. На примере префрактала первого порядка, наложенного на префрактал нулевого порядка (треугольник) можно видеть равенство площадей под кривой Кушелева (синий цвет) и над кривой (красный цвет).

 Форма печенья - фрактал другого типа...

Построение кривой Кушелева. Первые четыре звена строятся на сторонах симметричной звезды. Пятое звено строится на перпендикуляре ко второму. Его длина равна длине других звеньев.

"Снежинка" Коха (префракталы первого, второго и третьего порядков).

Обратите внимание, что в "печенье" Кушелева в отличие от "снежинки" Коха насчитывается не 4, а 5 звеньев ломаной, образующей элемент префрактала второго порядка.

"Печенье" Кушелева (префрактал второго порядка)

Префрактал второго порядка.

Кто построит префрактал третьего порядка?

 

Кельтский крест может быть представлен разностным фракталом Кушелева.

Подробнее.

---

Программа "Параметрический яйцис".

Кушелев: Определение: Яйцис - результат преобразования эллипса, при котором концы длинной оси остаются на месте, а концы короткой смещаются вдоль длинной на расстояние от нуля до полуоси. Промежуточные точки эллипса смещаются в том же направлении на расстояния пропорциональное разности проекций текущей точки и конца короткой оси. За начало отсчёта принимается ближайший конец длинной оси.

Neophyte: Нате вам. "Новое слово в математике". Построено за 3 минуты без аппроксимации.

Меняя пару коэффициентов легко строится галерея яйцисов любой, желаемой степени яйцистости...

Кушелев: О! Это то, что нужно! А как Вам это удалось?

Neophyte: Если упрощенно, строите в цикле:
x=sin(i)^k
y=cos(i)

Кушелев: Похоже, что Вы угадали, т.к. Ваша фигура больше похожа на формы некоторых инопланетных резонаторов, чем овоид...

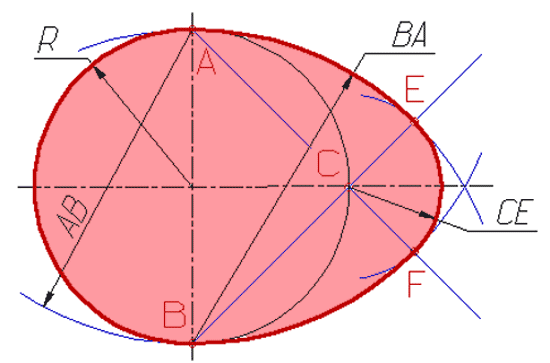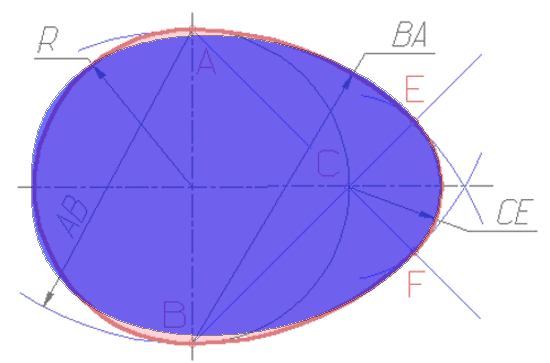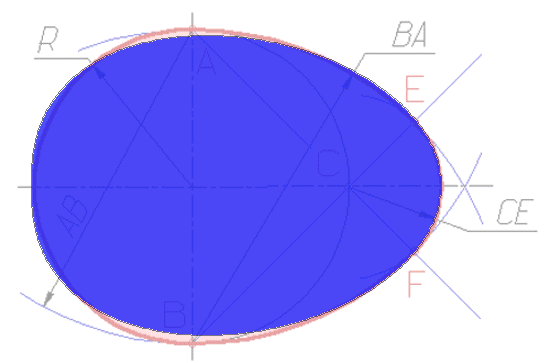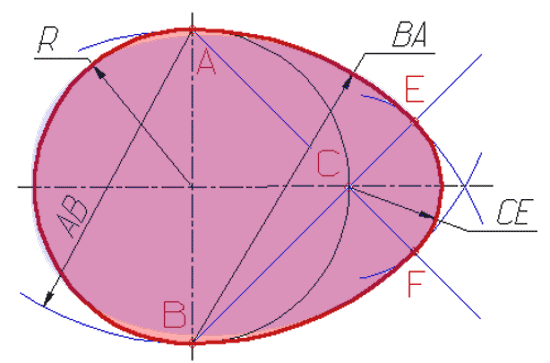
Вспоминаете формы гербов?

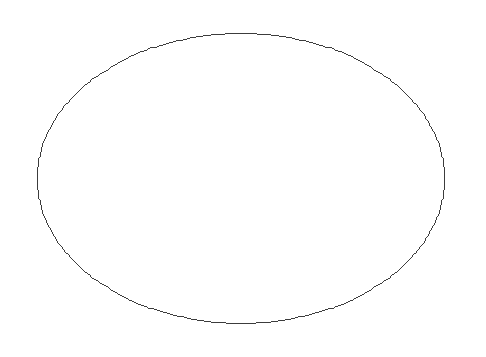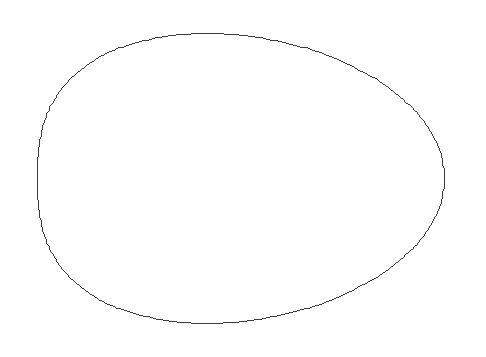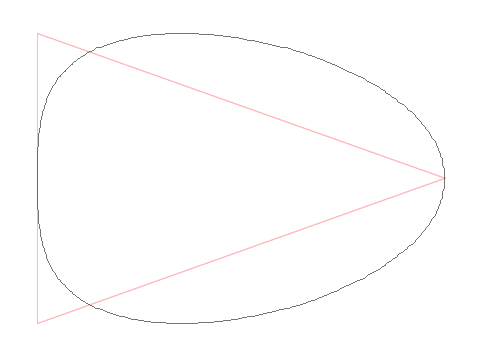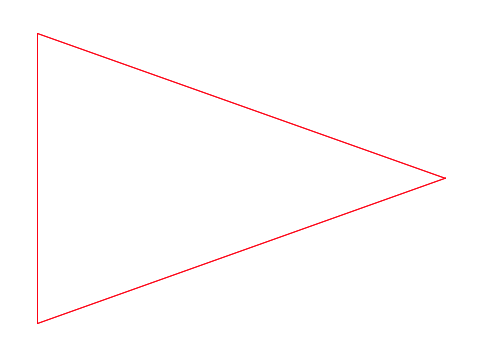
Итак, алгоритм построения идеального яйциса заключается в том, что концы большой полуоси эллипса остаются на своих местах, а концы малой полуоси смещаются максимально вдоль большой полуоси. При этом промежуточные точки эллипса смещаются пропорционально разности проекций на большую ось.

Как видим, в пределе эллипс превращается в равнобедренный треугольник.

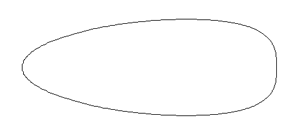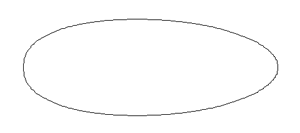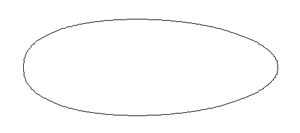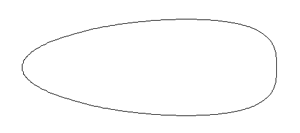
Изменение степени яйцистости вдоль длинной оси.

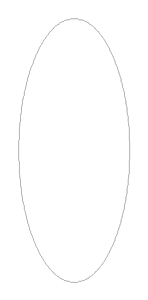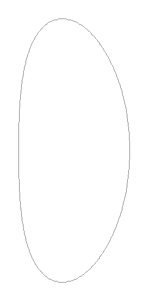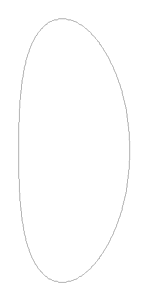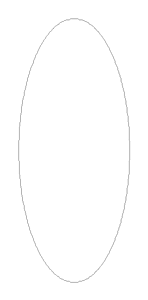
Деформацию вдоль короткой оси эллипса назовём "антияйцис" или "почка". "Туфелька рококо" является комбинацией преобразований "яйцис" и "почка". Преобразование может быть гипертрофировано, т.е. ось, вдоль которой происходит деформация, может сокращаться, например, в два раза и смещаться, например, на полуось в обратном направлении.

При этом оптимальные параметры, вероятно, можно определить лишь экспериментально, т.е. изготавливая источники энергии в стиле рококо и сравнивая их мощности.

Мы с Вами сейчас работаем с азами деформации резонансных систем.

Вот результат более сложной деформации:

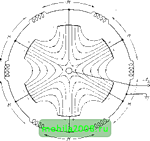
Вы можете себе представить, каким образом была получена эта форма из более простой?

Была многозаходная спираль Архимеда, точнее Рисса-Кноченхауэра-Кушелева.

Далее круг был разбит на кольцевые полосы. А дальше нечётные окружности повернулись на определённый угол, а промежуточные точки спиралей сдвинулись по окружностям пропорционально разности радиусов с опорными точками.

В результате такого преобразования мощность микроволнового источника энергии существенно увеличивается.

Любопытно, но такие преобразования тоже встречаются в инопланетной технике.

Но мне интересно посмотреть комбинированные преобразования, например, "яйцис" + "почка". Дадут ли они "туфельку рококо"?

 Подробнее.

Подробнее

Вот эта форма, похоже, получена путём преобразования окружности в треугольник. Среднее между "яйцисом" и "почкой".

Так работает преобразование "яйцис" и "почка" по отдельности.

А как они будут комбинироваться?

Не, второе преобразование "почка" неправильное. Это не "почка". В результате вместо "туфельки рококо" получилась устрица

Могут ли существовать формулы или алгоритмы, описывающие "туфельку рококо"?

Этих "туфелек" в действительности, как вы уже догадались, тоже целый класс...

Тут добрые люди написали программку: http://www.webmath.ru/web/prog31_1.php

Функцию, которая выглядит похожей на яйцис, подобрать, конечно, можно.
Но интересно найти функцию, которая точно совпадёт с формой инопланетной техники

 

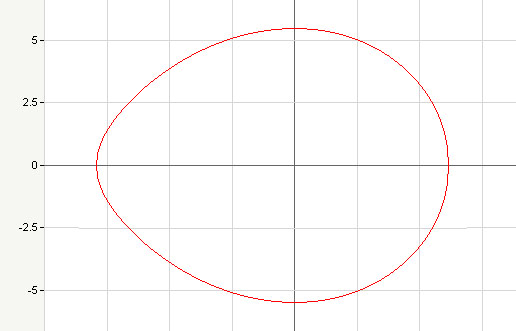
Вроде форма похожа, но функция мне не нравится...

Формула эллипса: x = cos(a) , y = k * sin(a)

Формула: x = cos(a) * abs(cos(a)), y = k  * sin(a) превращает эллипс в известную по иконам форму.

Слегка изменим формулу: x = cos(a), y = k  * sin(a) * abs(cos(a)) эллипс превращается в другую известную по иконам форму (восьмёрку) ...

Случайны ли эти формы, построенные по формулам? Функция abs фактически моделирует зеркало, т.е. описывает зеркально-симметричную фигуру. А мы знаем, что симметрия - основа резонансных систем...

Превращение эллипса в треугольник вроде получается, но может быть просто похоже, но не то...

Сферические элементы яйциса помогают понять, что в пределе получится не треугольник, а пятиугольник...

Флоренция (Firenze или Fiorenza)

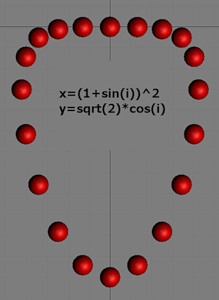
x=(1+sin(i))^2
y=sqrt(2)*cos(i)

Не является ли контур этого герба асимптотой яйциса?

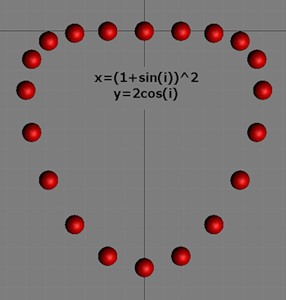
x=(1+sin(i))^2
y=2cos(i)

Материал с форума лаборатории Наномир:

 diprospan: Овалы Кассини

Кушелев: Ух ты! Может быть это - правильные яйцисы?

Цитата: Овал Кассини — геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату некоторого числа a.

Частным случаем овала Кассини при фокусном расстоянии равном 2a является Лемниската Бернулли. Сам овал является лемнискатой с двумя фокусами.

Кривая была придумана астрономом Джовании Кассини. Он ошибочно считал, что она точнее определяет орбиту Земли, чем эллипс[1].

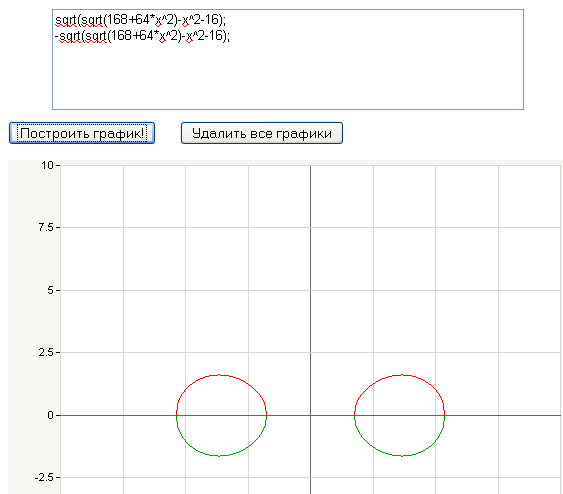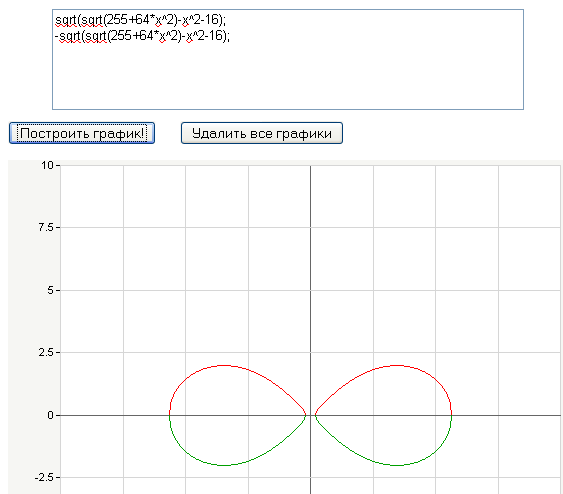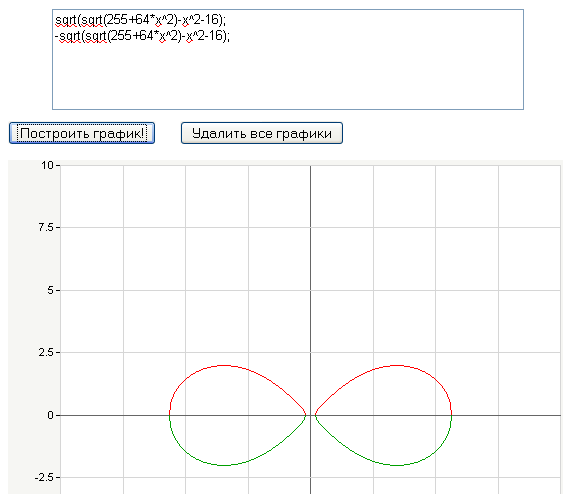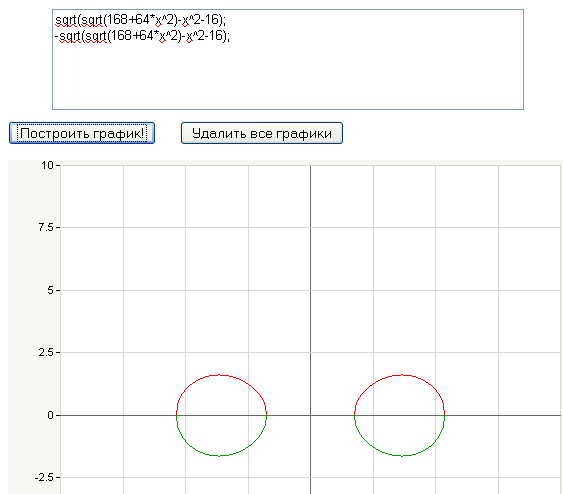
Овал Кассини что-то не очень похож по пропорциям на яйцевидный герб...

Подробнее

Любопытно, что восьмёрка тоже является формой резонатора. Так что овалы Кассини дважды подходят

Но на самом деле, резонаторы в форме яйца, в т.ч. плоские яйцисы могут быть разной формы. И восьмёрки могут быть с одинаковыми половинками и разными. Так что овалы Кассини дают лишь два частных случая: резонатор-яйцис и резонаторов-восьмёрка. Оба варианта с конкретными параметрами.

Должны быть обобщённые алгоритмы, которые описывают широкие классы резонаторов этих двух типов и других...

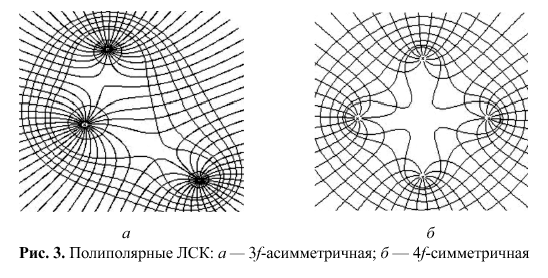
Кушелев: Очень интересно... Выходит, что резонатор в форме креста может быть описан в такой системе координат одной лемнискатой

x=(1.414+sin(i))^2
y=2(1.414+cos(i))^2

Кушелев: Благодарю!

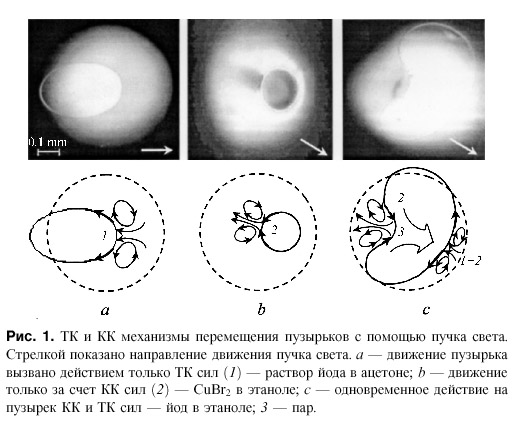
В электромагнитном резонаторе стиля рококо тоже протекают процессы, похожие на гидродинамические. Об этом свидетельствует "завиток" в этой зоне:

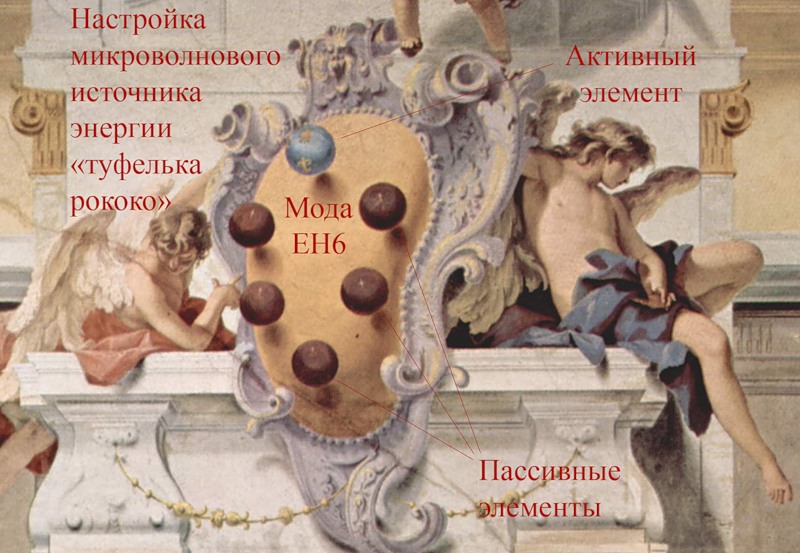
У оригинальной "туфельки рококо" есть вогнутый участок...

Похоже, что она сделана из яйциса неким преобразованием типа чем дальше от некого центра расположена точка фигуры, тем слабее она отодвигается от него.

Дальняя от некого центра часть яйциса практически не изменила форму, а ближняя часть из выпуклой стала вогнутой...

Кстати, то же преобразование, что из "яйциса" делает "туфельку рококо", из "круга" делает "почку" или "фасоль"

Подробнее

Любопытный герб, изображающий источник энергии, построенный с применением того же преобразования, что и "туфелька рококо"

Обсуждение.

 Применение фрактальных поверхностей для упаковки товаров массового производства

Материал с форума лаборатории Наномир:

Кушелев: Пока потенциальные инвесторы лаборатории Наномир думают, открывать финансирование или повременить, я решил перевести лабораторию Наномир на самофинансирование.

Для этого достаточно продать лицензии на упаковку продуктов питания, что принесёт производителям упаковки много миллионов долларов прибыли.

Но в процессе подготовки материалов для производителей упаковки я понял, что за этой технологией стоят фундаментальные, т.е. бесценные идеи, которые должны быть опубликованы независимо от патентования результатов прикладных исследований.

Дело в том, что фрактальная упаковка может применяться не только для упаковки продуктов повседневного спроса, но и для упаковки, например, отравляющих веществ, которые могут привести к катастрофе при транспортировке.

Фрактальная упаковка может применяться не только к веществу в твёрдой, жидкой и газообразной фазе, но и к плазме. Ведь магнитные ловушки для плазмы тоже можно сделать фрактальными...

Короче, я решил опубликовать теорию фрактальной упаковки веществ в разных агрегатных состояниях и полей(!), не раскрывая при этом Ноу-Хау для применения в быту и военных целях. Это достаточно объёмная тема, поэтому ей будет посвещен целый ряд выпусков рассылки "Новости лаборатории Наномир".

Параллельно начинаются переговоры с производителями упаковки, которые могут получить многомиллионные прибыли, если первыми начнут производство фрактальной упаковки для товаров массового производства.

Пример фрактальной поверхности, которая может использоваться для некоторых видов упаковок товаров массового производства...

Эксперт: Так Вы же раскрыли Ноу-Хау!

Кушелев: Вовсе нет. Это всего лишь бесплатная, рекламная часть Ноу-Хау. Самое сложное - не сама фрактальная поверхность, а способ сопряжения таких поверхностей, скажем для образования параллелепипеда. Дело в том, что края фрактальной поверхности неровные и сделать из таких поверхностей, например, кубик, нельзя. Но я знаю способ, при котором получается идеальный кубик, все его грани строго сопряжены, и его можно использовать для упаковки, скажем, воды, которая при замерзании увеличивается в объёме на 4%. Кубик, конечно, чуть-чуть увеличится в размерах, но не изменит формы. При этом он может быть сделан из такого материала, который существенно дешевле применяющихся сегодня. Если такой кубик уронить, то он может выдержать в несколько раз бОльшие ускорения, чем кубик из того же материала, но с плоскими гранями. Другими словами, если обычный пакет упадёт на пол, то может разорваться, а фрактальный нет. При тех же параметрах материала. Изготовители упаковки вынуждены делать упаковку толще, чем это необходимо в случае фрактальной поверхности. Причём в разы...

Потенциальный инвестор: Я правильно понял, что Вы опустились с уровня фрактальных выпаривательных комплексов инопланетян до банальной упаковки продуктов питания?

Кушелев: Правильная математика может быть использована в любой области человеческой деятельности. Если сознание инвесторов не готово к добыче драгметаллов миллионами тонн в год, но готово к выпуску молочных пакетов другой формы, то почему бы не заработать на этом несколько сотен тысяч долларов, которых мне хватит для создания микроволновой энергетики ("вечных лампочек"), транспорта ("летающих тарелок"), инструментов (трезубцев, ваджр), эликсира "вечной молодости"... ?

Естественно, что пожилые инвесторы, которые могли бы стать вечно-молодыми, рискуют при этом умереть от старости, т.к. время для них будет упущено, но мне-то что? У меня запас по времени есть :)

Обсуждение на форуме лаборатории Наномир.